题目内容
18.如图所示,用火柴杆摆出一系列三角形图案,按这种方式摆下去,当摆到20层(N=20)时,需要多少根火柴?
分析 关键是通过归纳与总结,得到其中的规律,按规律求解.
解答 解:n=1时,有1个三角形,需要火柴的根数为:3×1;
n=2时,有5个三角形,需要火柴的根数为:3×(1+2);
n=3时,需要火柴的根数为:3×(1+2+3);
…;
n=20时,需要火柴的根数为:3×(1+2+3+4+…+20)=630.
点评 此题考查的知识点是图形数字的变化类问题,本题的关键是弄清到底有几个小三角形.

练习册系列答案
相关题目
9.当$\sqrt{x}+\sqrt{y}=\sqrt{5}-\sqrt{3},\sqrt{xy}=\sqrt{15}-\sqrt{3}$时,x+y的值为( )
| A. | 2 | B. | 5 | C. | $8-2\sqrt{15}$ | D. | $8-4\sqrt{15}+2\sqrt{3}$ |
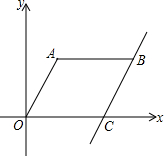 如图,已知点C坐标为(6,0),将线段OC向右平移3个单位,再向上平移4个单位得到线段AB,连接OA,此时OA=5.
如图,已知点C坐标为(6,0),将线段OC向右平移3个单位,再向上平移4个单位得到线段AB,连接OA,此时OA=5.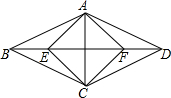 如图,菱形ABCD中,点E、F在对角线BD上,BE=DF=$\frac{1}{4}$BD,若四边形AECF为正方形,则tan∠ABE=$\frac{1}{2}$.
如图,菱形ABCD中,点E、F在对角线BD上,BE=DF=$\frac{1}{4}$BD,若四边形AECF为正方形,则tan∠ABE=$\frac{1}{2}$. 根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为8.
根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为8.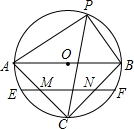 如图,⊙O的直径AB=8,P是圆上任一点(A,B除外),∠APB的平分线交⊙O于C,弦EF过AC,BC的中点M,N,则EF的长是4$\sqrt{3}$.
如图,⊙O的直径AB=8,P是圆上任一点(A,B除外),∠APB的平分线交⊙O于C,弦EF过AC,BC的中点M,N,则EF的长是4$\sqrt{3}$.