题目内容
14. 已知:如图,在四边形ABCD中,A′B′∥AB,A′D′∥AD,求证:△ABD∽△A′B′D′.
已知:如图,在四边形ABCD中,A′B′∥AB,A′D′∥AD,求证:△ABD∽△A′B′D′.
分析 由平行线得出$\frac{AB}{A′B′}=\frac{AC}{A′C}$,∠BAC=∠B′A′C,$\frac{AD}{A′D′}=\frac{AC}{A′C}$,∠DAC=∠D′A′C,得出$\frac{AB}{A′B′}=\frac{AD}{A′D′}$,∠BAD=∠B′A′D′,由相似三角形的判定方法即可得出结论.
解答 证明:∵A′B′∥AB,A′D′∥AD,
∴$\frac{AB}{A′B′}=\frac{AC}{A′C}$,∠BAC=∠B′A′C,$\frac{AD}{A′D′}=\frac{AC}{A′C}$,∠DAC=∠D′A′C,
∴$\frac{AB}{A′B′}=\frac{AD}{A′D′}$,∠BAD=∠B′A′D′,
∴△ABD∽△A′B′D′.
点评 本题考查了相似三角形的判定方法、平行线分线段成比例定理、平行线的性质;熟练掌握相似三角形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
4.下列语句中正确的是( )
| A. | x2+1是二次单顶式 | B. | -m2的次数是2,系数是1 | ||
| C. | 3x-25为五次二项式 | D. | -$\frac{3{x}^{2}{y}^{2}z}{2}$的系数是-$\frac{3}{2}$,次数是5 |
9.当$\sqrt{x}+\sqrt{y}=\sqrt{5}-\sqrt{3},\sqrt{xy}=\sqrt{15}-\sqrt{3}$时,x+y的值为( )
| A. | 2 | B. | 5 | C. | $8-2\sqrt{15}$ | D. | $8-4\sqrt{15}+2\sqrt{3}$ |
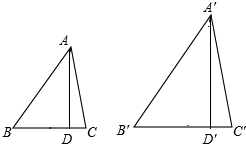 如图所示,已知△ABC与△A′B′C′,AD⊥BC于D,A′D′⊥B′C′于D′,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′,试说明△ABC∽△A′B′C′.
如图所示,已知△ABC与△A′B′C′,AD⊥BC于D,A′D′⊥B′C′于D′,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′,试说明△ABC∽△A′B′C′.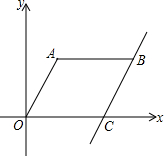 如图,已知点C坐标为(6,0),将线段OC向右平移3个单位,再向上平移4个单位得到线段AB,连接OA,此时OA=5.
如图,已知点C坐标为(6,0),将线段OC向右平移3个单位,再向上平移4个单位得到线段AB,连接OA,此时OA=5.