已知a-b=4.求代数式$\frac{{a}^{2}+{b}^{2}}{2}$-ab的值．题目和参考答案——青夏教育精英家教网—

题目内容

13．已知a-b=4，求代数式$\frac{{a}^{2}+{b}^{2}}{2}$-ab的值．

分析原式通分并利用同分母分式的减法法则变形，分解因式后将a-b的值代入计算即可求出值．

解答解：∵a-b=4，
∴原式=$\frac{{a}^{2}+{b}^{2}-2ab}{2}$=$\frac{（a-b）^{2}}{2}$=8．

点评此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．

练习册系列答案

相关题目

3．一元二次方程x²-6x=-9的根的情况是（　　）

	A．	有两个相等的实数根		B．	有两个不相等实数根
	C．	无实数根		D．	无法确定

4．下列语句中正确的是（　　）

	A．	x²+1是二次单顶式		B．	-m²的次数是2，系数是1
	C．	3x-2⁵为五次二项式		D．	-$\frac{3{x}^{2}{y}^{2}z}{2}$的系数是-$\frac{3}{2}$，次数是5

8．若m+n=7，mn=12，则m²+n²的值是（　　）

5．如果（m-3）xyⁿ⁺¹是一个关于x，y的五次单项式，则m，n应满足的条件为m≠3，n=3．

2．-5x²-5x+7+（3x²-2x-6）=-2x²-7x+1．

8．

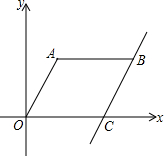如图，已知点C坐标为（6，0），将线段OC向右平移3个单位，再向上平移4个单位得到线段AB，连接OA，此时OA=5．
（1）求四边形OABC的面积；
（2）过点A作AD⊥x轴，垂足为点D，P是从O出发以每秒1个单位的速度向x轴正方向运动，Q是直线BC上一点，当△PCQ与△OAD全等时，求t的值．

试题分类