题目内容
15.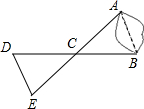 如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座水房D,在BD的中点C处有一棵百年古树,小明从A出发,沿直线AC一直向前经过点C走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量点E到水房D的距离,则DE的长度就是A、B两点之间的距离.
如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座水房D,在BD的中点C处有一棵百年古树,小明从A出发,沿直线AC一直向前经过点C走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量点E到水房D的距离,则DE的长度就是A、B两点之间的距离.(1)你能说明小明这样做的根据吗?
(2)如果小明未带测量工具,但是知道水房和点A到古树的距离分别为140米和100米,他能不能确定AB的长度范围?
分析 (1)可以利用SAS定理证明△DCE≌△BCA,根据全等三角形的性质可得AB=DE;
(2)根据三角形的三边关系定理可得BC-AC<AB<AC+BC,然后再代入数进行计算即可.
解答 解:(1)∵C为BD中点,
∴DC=BC,
在△ACB和△ECD中,
$\left\{\begin{array}{l}{AC=CE}\\{∠BCA=∠DCE}\\{DC=BC}\end{array}\right.$,
∴△DCE≌△BCA(SAS),
∴AB=DE,
∴DE的长度就是A、B两点之间的距离;
(2)由题意得:CD=140米,CA=100米,
∵DC=BC,
∴BC=140米,
∴BC-AC<AB<AC+BC,
∴40米<AB<240米.
点评 此题主要考查了三角形的三边关系,以及全等三角形的判定与性质,解决此题的关键是巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
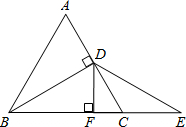 △ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,过点D作DF⊥BE于F.探究FC与BE间的数量关系,并证明.
△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,过点D作DF⊥BE于F.探究FC与BE间的数量关系,并证明.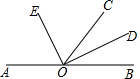 如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC
如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC
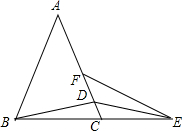 如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.