题目内容
6.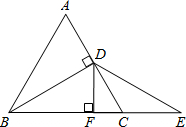 △ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,过点D作DF⊥BE于F.探究FC与BE间的数量关系,并证明.
△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,过点D作DF⊥BE于F.探究FC与BE间的数量关系,并证明.
分析 先根据△ABC是等边三角形,BD⊥AC可知∠DBE=30°,∠ACB=60°,再根据CE=CD可知∠CDE=∠E,由三角形外角的性质可知∠ACB=∠E+∠CDE=60°,故∠E=30°,故可得出∠E=∠DBE=30°,故BD=DE,再根据DF⊥BE可知BF=EF,即BF=$\frac{1}{2}$BE,由∠DFC=90°,∠ACB=60°,得到∠FDC=30°,根据直角三角形的性质得到CF=$\frac{1}{2}$CD=$\frac{1}{2}$CE,推出CF=$\frac{1}{3}$EF,即可得到结论.
解答 证明:∵△ABC是等边三角形,BD⊥AC,
∴∠DBE=30°,∠ACB=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB是△CDE的外角,
∴∠ACB=∠E+∠CDE=60°,
∴∠E=30°,
∴∠E=∠DBE=30°,
∴BD=DE,
∴△BDE是等腰三角形,
∵DF⊥BE,
∴BF=EF,即BF=$\frac{1}{2}$BE,
∵∠DFC=90°,∠ACB=60°,
∴∠FDC=30°,
∴CF=$\frac{1}{2}$CD=$\frac{1}{2}$CE,
∴CF=$\frac{1}{3}$EF,
∴CF=$\frac{1}{6}$BE.
点评 本题考查的是等边三角形的性质及三角形外角的性质,根据题意得出△BDE是等腰三角形是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16. 用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )
用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )
 用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )
用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )| A. | $\frac{2}{3}$m2 | B. | 1m2 | C. | $\frac{3}{2}$m2 | D. | 3m2 |
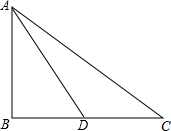 如果一个三角形一边上的中线长恰好等于这边的长,那么这个三角形称为“有趣三角形”,这条中线称为“有趣中线”.如图,已知Rt△ABC中,∠B=90°,若Rt△ABC是“有趣三角形”,AD为“有趣中线”,且AD=14cm,则AC=9$\sqrt{3}$cm.
如果一个三角形一边上的中线长恰好等于这边的长,那么这个三角形称为“有趣三角形”,这条中线称为“有趣中线”.如图,已知Rt△ABC中,∠B=90°,若Rt△ABC是“有趣三角形”,AD为“有趣中线”,且AD=14cm,则AC=9$\sqrt{3}$cm. 在数轴上表示a,b,0三数点的位置如图所示化简:$\sqrt{(a+b)^{2}}$-|a-b|.
在数轴上表示a,b,0三数点的位置如图所示化简:$\sqrt{(a+b)^{2}}$-|a-b|.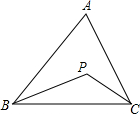 如图,已知点P是△ABC内一点,连结PB、PC,求证:
如图,已知点P是△ABC内一点,连结PB、PC,求证: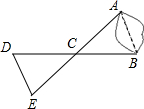 如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座水房D,在BD的中点C处有一棵百年古树,小明从A出发,沿直线AC一直向前经过点C走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量点E到水房D的距离,则DE的长度就是A、B两点之间的距离.
如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座水房D,在BD的中点C处有一棵百年古树,小明从A出发,沿直线AC一直向前经过点C走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量点E到水房D的距离,则DE的长度就是A、B两点之间的距离.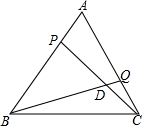 如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点A、C同时出发,运动速度均为1cm/s,点P从点A出发,沿A→B运动,到点B停止,点Q从点C出发,沿C→A运动,到点A停止,连接BQ、CP相交于点D,设点P的运动时间为x(s).
如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点A、C同时出发,运动速度均为1cm/s,点P从点A出发,沿A→B运动,到点B停止,点Q从点C出发,沿C→A运动,到点A停止,连接BQ、CP相交于点D,设点P的运动时间为x(s).