题目内容
10.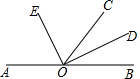 如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC
如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC(1)指出图中∠AOD与∠BOE的补角;
(2)求∠DOE的度数;
(3)说明∠COD与∠COE具有怎样的数量关系.
分析 (1)根据互为补角的和等于180°找出即可;
(2)根据角平分线的定义解答即可;
(3)根据角平分线的定义表示出∠COD与∠EOC,然后整理即可得解.
解答 解:(1)∠AOD的补角为∠BOD,∠BOE的补角为∠AOE;
(2)∵OD平分∠BOC,∠BOC=68°,
∴∠COD=$\frac{1}{2}$∠BOC,
∵OE平分∠AOC,
∴∠EOC=$\frac{1}{2}$∠AOC;
∴∠DOE=∠COD+∠EOC=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$×180°=90°;
(3)∵OD平分∠BOC,∠BOC=68°,
∴∠COD=$\frac{1}{2}$∠BOC,
∵OE平分∠AOC,
∴∠EOC=$\frac{1}{2}$∠AOC;
∴∠DOE=∠COD+∠EOC=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$×180°=90°,
∴∠COD与∠EOC互余.
点评 本题考查了余角和补角的概念,角度的计算,以及角平分线的定义,准确识图并熟记概念是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
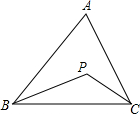 如图,已知点P是△ABC内一点,连结PB、PC,求证:
如图,已知点P是△ABC内一点,连结PB、PC,求证: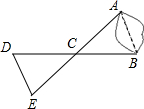 如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座水房D,在BD的中点C处有一棵百年古树,小明从A出发,沿直线AC一直向前经过点C走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量点E到水房D的距离,则DE的长度就是A、B两点之间的距离.
如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座水房D,在BD的中点C处有一棵百年古树,小明从A出发,沿直线AC一直向前经过点C走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量点E到水房D的距离,则DE的长度就是A、B两点之间的距离.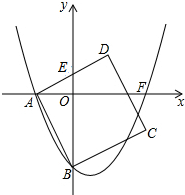 如图,二次函数y=ax2+bx-4m(a>0)与x轴负半轴交于点A,与y轴负半轴交于点B,正方形ABCD的边AD与y轴正半轴交于E(0,m).
如图,二次函数y=ax2+bx-4m(a>0)与x轴负半轴交于点A,与y轴负半轴交于点B,正方形ABCD的边AD与y轴正半轴交于E(0,m).