题目内容
17.已知实数x,y满足x+2y=4,并且x≤3,y<2,现有m=x-2y,则m的取值范围是-4<m≤2.分析 先把x+2y=4变形得到y=$\frac{1}{2}$(4-x),由y<2得到$\frac{1}{2}$(4-x)<2,解得x>0,所以x的取值范围为0<x≤3,再用x变形m得到m=2x-4,然后利用一次函数的性质确定m的范围.
解答 解:∵x+2y=4,
∴y=$\frac{1}{2}$(4-x),
∵y<2,
∴$\frac{1}{2}$(4-x)<2,解得x>0,
又∵x≤3,
∴0<x≤3,
∵m=x-2y=x-2×$\frac{1}{2}$(4-x)=2x-4,
当x=0时,m=-4;
当x=3时,m=2×3-4=2,
∴-4<m≤2.
故答案为:-4<m≤2.
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本步骤为:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.也考查了代数式的变形和一次函数的性质.

练习册系列答案
相关题目
7.已知a>b,则下列不等式错误的是( )
| A. | a-b>0 | B. | -3a<-3b | C. | a+2>b+2 | D. | 5-a>5-b |
12.已知正方形ABCD的边长为1,E、F分别为BC、CD上的点,且满足BE=CF,则△AEF的面积的最小值是( )
| A. | $\frac{\sqrt{2}}{8}$ | B. | $\frac{\sqrt{3}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |
6.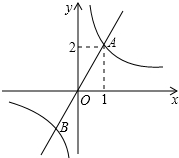 如图,函数y1=$\frac{{k}_{1}}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{{k}_{1}}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
 如图,函数y1=$\frac{{k}_{1}}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{{k}_{1}}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )| A. | x>l | B. | -1<x<0 | C. | -l<x<0 或x>l | D. | x<-1 或 0<x<1 |
 如图,在四边形ABCD中,对角线AC⊥BD,且AC=8,BD=10,E,F分别是边AB,CD的中点,则EF=$\sqrt{41}$.
如图,在四边形ABCD中,对角线AC⊥BD,且AC=8,BD=10,E,F分别是边AB,CD的中点,则EF=$\sqrt{41}$. 如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为42.
如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为42. 在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )
在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )