题目内容
9. 如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为42.
如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为42.
分析 如图,作∠ADO的平分线DP交AC于P,作PE⊥AD于E.由△POD∽△BOC,得$\frac{OP}{OB}$=$\frac{OD}{OC}$,设OP=x,推出OD=2x,由PE⊥AD,PO⊥DO,∠PDE=∠PDO,推出PE=OP,由$\frac{{S}_{△ADP}}{{S}_{△DPO}}$=$\frac{AP}{OP}$=$\frac{\frac{1}{2}•AD•PE}{\frac{1}{2}•DO•OP}$,推出$\frac{AD}{2x}$=$\frac{4-x}{x}$,推出AD=2(4-x),在Rt△ADO中,根据AD2=AO2+DO2,可得4(4-x)2=4x2+42,求出x的值,再根据S四边形ABCD=S△ABD+S△BDC=$\frac{1}{2}$•BD•AO+$\frac{1}{2}$•BD•OC=$\frac{1}{2}$•BD(OA+OC)计算即可.
解答 解:如图,作∠ADO的平分线DP交AC于P,作PE⊥AD于E.
∵∠ADO=2∠BCO,
∴∠PDO=∠BCO,
∵∠POD=∠BOC,
∴△POD∽△BOC,
∴$\frac{OP}{OB}$=$\frac{OD}{OC}$,设OP=x,
∴$\frac{x}{4}$=$\frac{DO}{8}$,
∴OD=2x,
∵PE⊥AD,PO⊥DO,∠PDE=∠PDO,
∴PE=OP,
∴$\frac{{S}_{△ADP}}{{S}_{△DPO}}$=$\frac{AP}{OP}$=$\frac{\frac{1}{2}•AD•PE}{\frac{1}{2}•DO•OP}$,
∴$\frac{AD}{2x}$=$\frac{4-x}{x}$,
∴AD=2(4-x),
在Rt△ADO中,∵AD2=AO2+DO2,
∴4(4-x)2=4x2+42,
∴x=$\frac{3}{2}$,
∴OD=3,
∴S四边形ABCD=S△ABD+S△BDC=$\frac{1}{2}$•BD•AO+$\frac{1}{2}$•BD•OC=$\frac{1}{2}$•BD(OA+OC)=$\frac{1}{2}$×7×12=42.
故答案为42.
点评 本题考查相似三角形的判定和性质、角平分线的性质、勾股定理、四边形的面积等知识,解题的关键是学会添加常用辅助线,学会构建方程解决问题,属于中考常考题型.

 如图为二次函数y=ax2+bx+c的图象,则下列说法中错误的是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法中错误的是( )| A. | ac<0 | B. | 2a+b=0 | ||
| C. | 对于任意x均有ax2+bx≥a+b | D. | 4a+2b+c>0 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
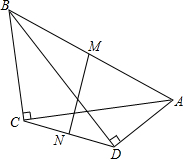 如图,∠ACB=∠ADB=90°,M、N分别为AB、CD的中点.求证:MN⊥CD.
如图,∠ACB=∠ADB=90°,M、N分别为AB、CD的中点.求证:MN⊥CD.