Question

12．已知正方形ABCD的边长为1，E、F分别为BC、CD上的点，且满足BE=CF，则△AEF的面积的最小值是（　　）

• A． $\frac{\sqrt{2}}{8}$
• B． $\frac{\sqrt{3}}{8}$
• C． $\frac{1}{4}$
• D． $\frac{3}{8}$

Answer 1

分析 如图，设BE=CF=x，则EC=DF=1-x．由题意可得S_△AEF=S_梯形AECD-S_△ADF-S_△EFC=$\frac{1+1-x}{2}$•1-$\frac{1}{2}$•1•（1-x）-$\frac{1}{2}$•x•（1-x）=$\frac{1}{2}$（x-$\frac{1}{2}$）²+$\frac{3}{8}$，构建二次函数的性质即可解决问题．

解答 解：如图，设BE=CF=x，则EC=DF=1-x．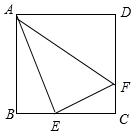

S_△AEF=S_梯形AECD-S_△ADF-S_△EFC=$\frac{1+1-x}{2}$•1-$\frac{1}{2}$•1•（1-x）-$\frac{1}{2}$•x•（1-x）=$\frac{1}{2}$（x-$\frac{1}{2}$）²+$\frac{3}{8}$，
∵$\frac{1}{2}$＞0，
∴x=$\frac{1}{2}$时，△AEF的面积有最大值，最大值为$\frac{3}{8}$，
故选D．

点评 本题考查正方形的性质、三角形的面积，二次函数等知识，解题的关键是学会构建二次函数解决最值问题，属于中考常考题型．