题目内容
18.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+1上的三点,则y1,y2,y3的大小关系为y1>y2>y3.分析 根据点A、B、C的横坐标利用二次函数图象上点的坐标特征即可求出y1、y2、y3的值,比较后即可得出结论.
解答 解:∵A(-2,y1)、B(1,y2)、C(2,y3)是抛物线y=-(x+1)2+1上的三点,
∴y1=0,y2=-3,y3=-8,
∵0>-3>-8,
∴y1>y2>y3.
故答案为:y1>y2>y3.
点评 本题考查了二次函数图象上点的坐标特征,根据点的坐标利用二次函数图象上点的坐标特征求出纵坐标是解题的关键.

练习册系列答案
相关题目
13.下列实数中的无理数是( )
| A. | π | B. | $\frac{1}{2}$ | C. | 0.62626262 | D. | -8 |
10.若点(a,6)关于原点的对称点是(-5,b),则a+b的值为( )
| A. | 1 | B. | -1 | C. | 11 | D. | -11 |
7.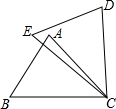 如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
 如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )| A. | ∠BCE=∠ACD | B. | AC=DC | C. | ∠A=∠D | D. | AB=DE |
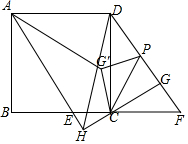 如图,正方形ABCD中,点E在BC边上,连接AE,过AD作DF∥AE交BC的延长线于点F,过点C作CG⊥DF于点G.延长AE、GC交于点H,点P是线段DG上的一点,连接CP,将△CPG沿CP翻折得到△CPG′,连接AG′,若CH=1,DH=3$\sqrt{2}$,则AG′长度的最小值是$\sqrt{26}$-2.
如图,正方形ABCD中,点E在BC边上,连接AE,过AD作DF∥AE交BC的延长线于点F,过点C作CG⊥DF于点G.延长AE、GC交于点H,点P是线段DG上的一点,连接CP,将△CPG沿CP翻折得到△CPG′,连接AG′,若CH=1,DH=3$\sqrt{2}$,则AG′长度的最小值是$\sqrt{26}$-2.