题目内容
13.科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况如下表:| 温度x/℃ | … | -4 | -2 | 0 | 2 | 4 | 4.5 | … |
| 植物每天高度增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 19.75 | … |
| A. | y=-x2-2x+49 | B. | y=-x2+2x+49 | C. | y=x2+2x-49 | D. | y=x2-2x+49 |
分析 设y=ax2+bx+c(a≠0),然后选择x=-2、0、2三组数据,利用待定系数法求二次函数解析式即可.
解答 解:设y=ax2+bx+c(a≠0),
∵x=-2时,y=49,
x=0时,y=49,
x=2时,y=41,
∴$\left\{\begin{array}{l}{4a-2b+c=49}\\{c=49}\\{4a+2b+c=41}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=49}\end{array}\right.$.
所以,y关于x的函数关系式为y=-x2-2x+49.
故选A.
点评 本题考查了根据实际问题列二次函数关系式,掌握待定系数法是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
2.下列结论正确的是( )
| A. | 若a2=b2,则a=b | B. | 若a>b,则a2>b2 | ||
| C. | 若a≠0,b≠0,则a2+b2>0 | D. | 若a≠b,则a2≠b2 |
 如图,已知BE⊥AC于点E,DE⊥AC于点F,BE=DF,AE=CF,求证:AB∥CD.
如图,已知BE⊥AC于点E,DE⊥AC于点F,BE=DF,AE=CF,求证:AB∥CD.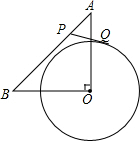 如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为2,点P是AB边上一动点,过P作⊙O的一条切线,切点为Q,求PQ的最小值和最大值.
如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为2,点P是AB边上一动点,过P作⊙O的一条切线,切点为Q,求PQ的最小值和最大值.