题目内容
17.观察下列一组等式的化简.然后解答后面的问题:$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$-$\sqrt{2}$;
$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{1×(\sqrt{4}-\sqrt{3})}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=2-$\sqrt{3}$…
(1)在计算结果中找出规律$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$(n表示大于0的自然数)
(2)通过上述化简过程,可知 $\sqrt{11}$-$\sqrt{10}$<$\sqrt{12}$-$\sqrt{10}$(填“>”、“<”或“=”).
分析 (1)根据题意归纳总结得到一般性规律,写出即可;
(2)利用作差法比较即可.
解答 解:(1)根据题意得:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;
(2)∵($\sqrt{11}$-$\sqrt{10}$)-($\sqrt{12}$-$\sqrt{10}$)=$\sqrt{11}$-$\sqrt{10}$-$\sqrt{12}$+$\sqrt{10}$=$\sqrt{11}$-$\sqrt{12}$<0,
∴$\sqrt{11}$-$\sqrt{10}$<$\sqrt{12}$-$\sqrt{10}$,
故答案为:<
点评 此题考查了分母有理化,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目

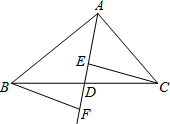 如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件DE=DF,使得△BDF≌△CDE,依据是SAS.
如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件DE=DF,使得△BDF≌△CDE,依据是SAS.