题目内容
6.在△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、BC边上,且DE∥AC.(1)问:$\frac{CE}{AD}$=$\frac{1}{2}$;
(2)若△BDE绕点B逆时针旋(如图2),试求$\frac{C{E}_{1}}{A{D}_{1}}$的值;
(3)若△BDE绕点B逆时针旋转α角度(0°<α≤180°)在旋转过程中,点D的对应点为D1,点E的对应点为E1,设直线D1E1与直线AB交于M,与直线AC交于N,是否存在这样的α使得三角形AMN为等腰三角形?若存在.直接写出α的度数;若不存在,说明理由.
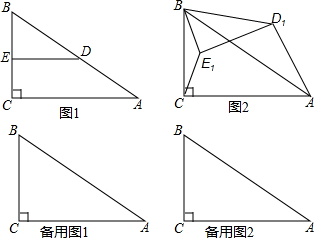
分析 (1)根据含30°的直角三角形的三边的关系,再直接代入求解即可,
(2)先由旋转和含30°的直角三角形的三边关系,得出$\frac{B{E}_{1}}{BC}=\frac{B{D}_{1}}{BD}$,从而判断出△BCE1∽△BAD1,即可;
(3)按边分AM=AN,MN=AM,MN=AN三种情况画出图形讨论计算即可.
解答 解:(1)在△ABC中,∠C=90°,∠A=30°,
∴AB=2BC,
∵DE∥AC,
∴∠BDE=∠A=30°,
∴BD=2BE;
∴$\frac{CE}{AD}=\frac{BC-BE}{AB-BD}$=$\frac{BC-BE}{2BC-2BE}$=$\frac{1}{2}$,
故答案为$\frac{1}{2}$;
(2)由旋转有,BD1=2BE1,
由(1)知,AB=2BC,
∴$\frac{B{E}_{1}}{BC}=\frac{B{D}_{1}}{BD}$
由旋转知,∠CBE1=∠ABD1,
∴△BCE1∽△BAD1,
∴$\frac{C{E}_{1}}{A{D}_{1}}=\frac{BC}{AB}$=$\frac{1}{2}$,
(3)如图1,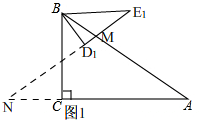
当MN=MA时,∠N=∠A=30°,
∴∠AMN=180°-∠A-∠N=120°,
∵∠BD1E1=90°,
∴∠MBD1=30°
∵∠ABC=60°
∴α=∠CBD1=∠ABC-∠MBD1=60°-30°=30°;
如图2,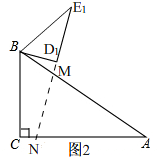
当AM=AN时,∠ANM=∠AMN=$\frac{1}{2}$(180°-∠A)=75°,
∵∠BD1M=90°,
∴∠ABD1=15°,
∵∠ABC=60°
∴α=∠CBD1=∠ABC+∠ABD1=75°,
如图3,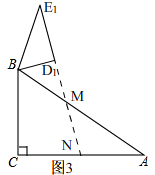
当NM=NA时,∠AMN=∠A=30°,
∵∠BD1M=90°,
∴∠ABD1=60°,
∵∠ABC=60°
∴α=∠ABC+∠ABD1=120°,
∴三角形AMN为等腰三角形的α为30°,75°,120°.
点评 此题是几何变换综合题,主要考查了含30°的直角三角形的性质,旋转的性质,相似三角形的判定和性质,等腰三角形的性质,解本题的根据是表示出含30°的直角三角形的三边的关系,作出图形是解本题的难点.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | 都为正 | B. | 都为负 | C. | 同号 | D. | 异号 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
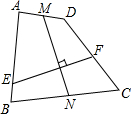 如图,四边形ABCD中,AB=CD,M,N分别为AD,BC的中点,EF⊥MN交AB于点E,交CD于点F.求证:∠AEF=∠DFE.
如图,四边形ABCD中,AB=CD,M,N分别为AD,BC的中点,EF⊥MN交AB于点E,交CD于点F.求证:∠AEF=∠DFE.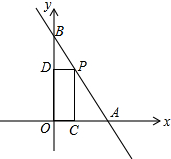 如图,一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A、B重合),过点P分别作OA和OB的垂线,垂足分别为C、D.
如图,一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A、B重合),过点P分别作OA和OB的垂线,垂足分别为C、D.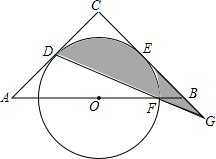 如图,已知△ABC,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC相切于点D,与BC相切于点E.⊙O交OB于F,连接DF并延长交CB的延长线于G.
如图,已知△ABC,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC相切于点D,与BC相切于点E.⊙O交OB于F,连接DF并延长交CB的延长线于G.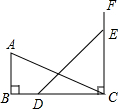 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,过点C作CF⊥BC,如果点D,E分别在BC、CF上运动,并始终保持DE=EC,那么当CD=6或8时,△ABC与△DCE全等.
如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,过点C作CF⊥BC,如果点D,E分别在BC、CF上运动,并始终保持DE=EC,那么当CD=6或8时,△ABC与△DCE全等.