题目内容
12.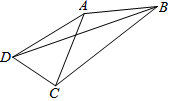 如图,在四边形ABCD中,∠ACB=∠ABC=30°,∠ADC=60°,AD=5,CD=3,则BD的长为2$\sqrt{21}$.
如图,在四边形ABCD中,∠ACB=∠ABC=30°,∠ADC=60°,AD=5,CD=3,则BD的长为2$\sqrt{21}$.
分析 根据旋转的性质得到AE=AD,∠EAD=120°,CE=BD,连接DE,过A作AH⊥DE于H,根据等腰三角形的性质得到DH=EH,∠ADH=30°,推出∠CDE=90°,根据勾股定理即可得到结论.
解答 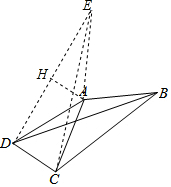 解:把△ABD绕着得A顺时针旋转120°得到△ACE,
解:把△ABD绕着得A顺时针旋转120°得到△ACE,
则AE=AD,∠EAD=120°,CE=BD,
连接DE,过A作AH⊥DE于H,
∴DH=EH,∠ADH=30°,
∵AD=5,
∴DH=$\frac{\sqrt{3}}{2}$AD=$\frac{5\sqrt{3}}{2}$,
∴DE=5$\sqrt{3}$,
∵∠ADC=60°,
∴∠CDE=90°,
∴CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=2$\sqrt{21}$.
∴BD=CE=2$\sqrt{21}$,
故答案为:2$\sqrt{21}$.
点评 本题考查了旋转的性质,勾股定理,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
13.在平面直角坐标系中,点A,B的坐标分别为(2m-2,3),(m,3),且点A在点B的左侧,若线段AB与直线y=-2x+1相交,则m的取值范围是( )
| A. | -1≤m≤$\frac{1}{2}$ | B. | -1≤m≤1 | C. | -$\frac{1}{2}$≤m≤1 | D. | 0≤m≤1 |
20.若x、y为有理数,且x≠0,若x+y=0,则($\frac{y}{x}$)2015的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2015 |
2.袋子中装有15个黑球、1个白球,它们除颜色外无其他差别,随机从袋子中摸出一个球,则下列说法正确的是( )
| A. | 这个球可能是白球 | |
| B. | 摸到黑球、白球的可能性的大小一样 | |
| C. | 这个球一定是黑球 | |
| D. | 事先能确定摸到什么颜色的球 |
 如图,已知AD⊥BC,EF⊥BC,∠4=∠C,试证明∠1=∠2.
如图,已知AD⊥BC,EF⊥BC,∠4=∠C,试证明∠1=∠2. 如图,已知AB⊥CD,EF⊥AB,∠DGC=105°,∠BCA=75°,请说明∠CEF+∠CDG=180°的理由.
如图,已知AB⊥CD,EF⊥AB,∠DGC=105°,∠BCA=75°,请说明∠CEF+∠CDG=180°的理由. 如图,DE⊥AC,∠AGF=∠ABC,∠GFB+∠BDE=180°,试判断BF与AC的位置关系,并说明理由.
如图,DE⊥AC,∠AGF=∠ABC,∠GFB+∠BDE=180°,试判断BF与AC的位置关系,并说明理由.