题目内容
6.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)设玩具的销售单价为x元(x>40);
则销售量为1000-10x件,销售玩具获得的利润为-10x2+1300x-30000元(用含x的多项式表示)
(2)商场为减少库存玩具,销售单价应定位多少元时,能获得1万元销售利润?
(3)若规定该品牌玩具装销售单价不低于45元,且商场要完成不少于520件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
分析 (1)根据题意即可得到结论;
(2)根据题意得方程求得x1=50,x2=80,为减少库存玩具,于是得到结论;
(3)根据题意得方程组,求得45≤x≤48,根据二次函数的性质得到当45≤x≤48时,y随x增大而增大,于是得到结论.
解答 解:(1)根据题意得;销售量为1000-10x件,销售玩具获得的利润为-10x2+1300x-30000元,
故答案为:1000-10x,-10x2+1300x-30000;
(2)根据题意得:-10x2+1300x-30000=10000,
解之得:x1=50,x2=80,
为减少库存玩具,所以取x1=50,
答:玩具销售单价为50元时,可获得10000元销售利润;
(3)根据题意得$\left\{\begin{array}{l}{1000-10x≥520}\\{x≥45}\end{array}\right.$,解得:44≤x≤46,
w=-10x2+1300x-30000=-10(x-65)2+12250,
∵a=-10<0,对称轴x=65,
∴当44≤x≤46时,y随x增大而增大,
∴当x=46时,W最大值=8240(元),
答:商场销售该品牌玩具获得的最大利润为8240元.
点评 本题考查了二次函数的应用:根据实际问题列出二次函数关系式,然后利用二次函数的性质,特别是二次函数的最值问题解决实际中的最大或最小值问题.

练习册系列答案
相关题目

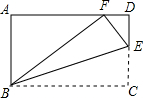 如图,在矩形ABCD中,E为CD边上的点,将△BCE沿BE折叠,点C恰好落在AD边上的点F处.
如图,在矩形ABCD中,E为CD边上的点,将△BCE沿BE折叠,点C恰好落在AD边上的点F处. 如图,?ABCD的对角线AC,BD相交于点O,点E是边AD的中点,若△BCD的周长为18,则△DEO的周长是9.
如图,?ABCD的对角线AC,BD相交于点O,点E是边AD的中点,若△BCD的周长为18,则△DEO的周长是9.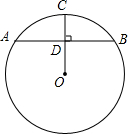 如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16.
如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16. 如图,AD平分△ABC的外角∠EAC,且AD∥BC,若∠BAC=82°,则∠B=49°.
如图,AD平分△ABC的外角∠EAC,且AD∥BC,若∠BAC=82°,则∠B=49°.