题目内容
1.下列各式中,正确的是( )| A. | $\frac{6-2x}{-x+3}$=2 | B. | $\frac{a-b}{(a-b)(a+b)}$=0 | C. | $\frac{(a-b)^{3}}{(b-a)^{3}}$=1 | D. | $\frac{(a-b)^{2}}{(b-a)^{2}}$=-1 |
分析 首先把分子或分母分解因式,然后找出分子和分母的公因式进行分解即可.
解答 解:A、$\frac{6-2x}{-x+3}$=$\frac{2(3-x)}{3-x}$=2,故此选项正确;
B、$\frac{a-b}{(a-b)(a+b)}$=$\frac{1}{a+b}$,故此选项错误;
C、$\frac{(a-b)^{3}}{(b-a)^{3}}$=-1,故此选项错误;
D、$\frac{(a-b)^{2}}{(b-a)^{2}}$=1,故此选项错误;
故选:A.
点评 此题主要考查了约分,关键是正确找出分子分母的公因式.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
11.抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
| A. | m≤2或m≥3 | B. | m≤3或m≥4 | C. | 2<m<3 | D. | 3<m<4 |
12.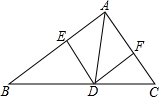 如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )
如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )
 如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )
如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD平分∠BAC,那么四边形AEDF是矩形 | |
| D. | 如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形 |
9.方程x+3y=5与下列哪个方程组合,使得方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$( )
| A. | 3x+2y=7 | B. | -2x+y=-3 | C. | 6x+y=8 | D. | 以上都不对 |
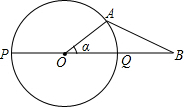 如图,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在⊙O的上半圆运动(含P、Q两点),连结AB,设∠AOB=α.有以下结论:
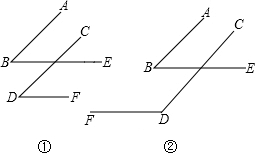
如图,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在⊙O的上半圆运动(含P、Q两点),连结AB,设∠AOB=α.有以下结论: 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=15°,那么∠2的度数是75°.
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=15°,那么∠2的度数是75°.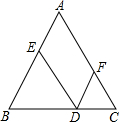 如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AC交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为24cm.
如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AC交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为24cm.