题目内容
9.方程x+3y=5与下列哪个方程组合,使得方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$( )| A. | 3x+2y=7 | B. | -2x+y=-3 | C. | 6x+y=8 | D. | 以上都不对 |
分析 把$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$代入A、B、C中的方程中,可使B左右相等,因此B正确.
解答 解:A、当$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$时,3x+2y≠7,故此选项错误;
B、当$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$时,-2x+y=-3,故此选项正确;
C、当$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$时,6x+y≠8,故此选项错误;
D、因为B正确,故此选项错误;
故选:B.
点评 此题主要考查了二元一次方程组的解,能同时使两个方程左右相等的方程的解就是方程组的解.

练习册系列答案
相关题目
20.用一副三角板的内角可以画出大于0°且小于180°的不同角度的角共有( )
| A. | 9种 | B. | 10种 | C. | 11种 | D. | 12种 |
17.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
①7cm,5cm,11cm ②4cm,3cm,7cm ③5cm,10cm,4cm ④2cm,3cm,1cm.
①7cm,5cm,11cm ②4cm,3cm,7cm ③5cm,10cm,4cm ④2cm,3cm,1cm.
| A. | ① | B. | ② | C. | ③ | D. | ④ |
1.下列各式中,正确的是( )
| A. | $\frac{6-2x}{-x+3}$=2 | B. | $\frac{a-b}{(a-b)(a+b)}$=0 | C. | $\frac{(a-b)^{3}}{(b-a)^{3}}$=1 | D. | $\frac{(a-b)^{2}}{(b-a)^{2}}$=-1 |
18. 已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
(1)观察表中各对应点坐标的变化,并填空:a=1,b=2,c=1;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是5.
 已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:| △ABC | A(a,0) | B(3,0) | C(5,5) |
| △A1B1C1 | A1(-3,2) | B1(-1,b) | C1(c,7) |
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是5.
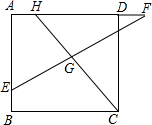 对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.
对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.
