题目内容
16.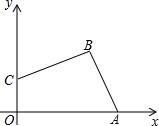 如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2)
如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2)(1)求S四边形ABCO;
(2)求S△ABC;
(3)在x轴上是否存在一点P,使S△PAB=10?若存在,请求点P坐标.
分析 (1)过点B作BD作BD⊥OA与点D,把四边形分割为直角梯形和直角三角形,即可解答;
(2)△ABC的面积=四边形ABCO的面积-△AOC的面积;
(3)存在,设点P(x,0),则PA=|x-4|,根据S△PAB=10,所以$\frac{1}{2}×|x-4|×4=10$,即可解答.
解答 解:(1)如图1,过点B作BD作BD⊥OA与点D,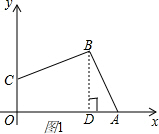
∵点A(4,0),B(3,4),C(0,2)
∴OC=2;,OD=3,BD=4,AD=4-3=1,
∴S四边形ABCO=S梯形CODB+S△ABD=$\frac{1}{2}×(2+4)×3+\frac{1}{2}×1×4$=9+2=11.
(2)如图2,连接AC,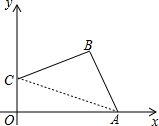
S△ABC=S四边形ABCO-S△AOC=11-$\frac{1}{2}×4×2$=11-4=7.
(3)存在,设点P(x,0),
则PA=|x-4|,
∵S△PAB=10,
∴$\frac{1}{2}×|x-4|×4=10$,
∴|x-4|=5,
解得:x=9或x=-1,
∴点P的坐标为(9,0)或(-1,0).
点评 本题考查了坐标与图形的性质,解决本题的关键是通过作辅助线,把四边形分割为直角梯形和直角三角形.

练习册系列答案
相关题目
11.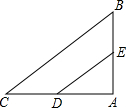 如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
 如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
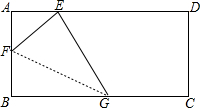 如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10,当折痕的另一端F在AB边上时,求△EFG的面积.
如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10,当折痕的另一端F在AB边上时,求△EFG的面积.
 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.