题目内容
2.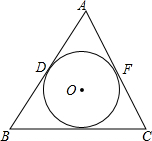 如图,⊙O内切于△ABC,切点分别为D、E、F
如图,⊙O内切于△ABC,切点分别为D、E、F(1)求证:∠BOC=90°+$\frac{1}{2}$∠BAC;
(2)若BC=4,AC=5,AB=6,求AD、BE、CF的长;
(3)若BC=a,AC=b,AB=c,当∠C=90°时,求内切圆的半径长.
分析 (1)如图,连接OB,OC,根据角平分线的性质得到∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,由三角形的内角和得到∠ABC+∠ACB=180°-∠A,等量代换即可得到结论;
(2)根据切线的性质得到AD=AF,BD=BE,CE=CF,列方程组即可得到结论;
(3)由(2)的结论即可得到结果.
解答  解:(1)如图,连接OB,OC,
解:(1)如图,连接OB,OC,
∵⊙O内切于△ABC,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∵∠ABC+∠ACB=180°-∠A,
∴∠BOC=180°-∠OBC-∠OCB=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠BAC;
(2)∵⊙O内切于△ABC,切点分别为D、E、F,
∴AD+BD=6,AF+CF=5,BE+CE=4,
∵AD=AF,BD=BE,CE=CF,
∴设AD=AF=x,BD=BE=y,CE=CF=z,
∴$\left\{\begin{array}{l}{x+y=6}\\{x+z=5}\\{y+z=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=3.5}\\{y=2.5}\\{z=1.5}\end{array}\right.$,
∴AD=3.5,BE=2.5,CF=1.5;
(3)由(2)可知:BE=$\frac{1}{2}$(c-b+a),CE=r=$\frac{1}{2}$(a+b-c),
即内切圆的半径为$\frac{1}{2}$(a+b-c).
点评 本题考查了三角形的内切圆与内心,三角形的内角和,切线的性质,解方程组,熟练掌握切线的性质是解题的关键.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| 永定区 | 武陵源区 | 慈利县 | 桑植县 |
| 32 | 32 | 33 | 30 |
| A. | 32℃,32℃ | B. | 32℃,33℃ | C. | 33℃,33℃ | D. | 32℃,30℃ |
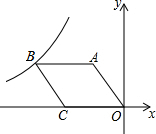 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B,则k的值为-32.
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B,则k的值为-32. 求不等式组$\left\{\begin{array}{l}5x-3<4x\\ 4(x+1)+2≥x\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.
求不等式组$\left\{\begin{array}{l}5x-3<4x\\ 4(x+1)+2≥x\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.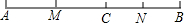 如图,点C在线段AB上,AC=8cm,CB=6cm,点M,N分别是AC,BC的中点.求线段MN的长.
如图,点C在线段AB上,AC=8cm,CB=6cm,点M,N分别是AC,BC的中点.求线段MN的长.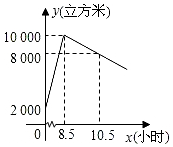 星期天8:00~8:30,燃气公司给加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.
星期天8:00~8:30,燃气公司给加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.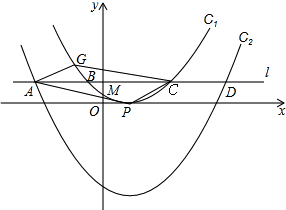
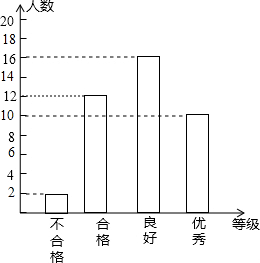 为了提高教师的综合素质,教育部门对全长沙市教师进行某项专业技能培训.为了解培训的效果,培训结束后随机抽取了部分参训老师进行技能测试,测试结果分成“不合格”、“合格”、“良好”、“优秀”四个等级,并绘制了如图所示的统计图,请根据统计图提供的信息,回答下列问题:
为了提高教师的综合素质,教育部门对全长沙市教师进行某项专业技能培训.为了解培训的效果,培训结束后随机抽取了部分参训老师进行技能测试,测试结果分成“不合格”、“合格”、“良好”、“优秀”四个等级,并绘制了如图所示的统计图,请根据统计图提供的信息,回答下列问题: