题目内容
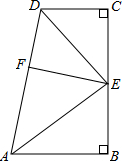 如图,∠B=∠C=90°,E是BC的中点,EF⊥AD于点F,DE平分∠ADC,∠CED=35°,则∠EAB=
如图,∠B=∠C=90°,E是BC的中点,EF⊥AD于点F,DE平分∠ADC,∠CED=35°,则∠EAB=考点:角平分线的性质
专题:
分析:根据角平分线上的点到角的两边距离相等可得CE=EF,然后求出EF=BE,再根据到角的两边距离相等的点在角的平分线上判断出AE平分∠BAD,根据直角三角形两锐角互余求出∠CDE,再求出∠ADC,然后求出∠BAD,再求解即可.
解答:解:∵DE平分∠ADC,∠C=90°,EF⊥AD于点F,
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴EF=BE,
∴AE平分∠BAD,
∵∠CED=35°,
∴∠CDE=90°-35°=55°,
∴∠ADC=2∠CDE=2×55°=110°,
∵∠B=∠C=90°,
∴AB∥CD,
∴∠BAD=180°-110°=70°,
∴∠EAB=
∠BAD=
×70°=35°.
故答案为:35°.
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴EF=BE,
∴AE平分∠BAD,
∵∠CED=35°,
∴∠CDE=90°-35°=55°,
∴∠ADC=2∠CDE=2×55°=110°,
∵∠B=∠C=90°,
∴AB∥CD,
∴∠BAD=180°-110°=70°,
∴∠EAB=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:35°.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,到角的两边距离相等的点在角的平分线上,直角三角形两锐角互余的性质和平行线的判定与性质,熟记各性质并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
以下列各组线段为边作三角形,不能构成直角三角形的是( )
A、1,
| ||||||
B、
| ||||||
| C、5,12,13 | ||||||
| D、9,40,41 |
 如图,AB是⊙O的直径,AM和BN是它的两条切线,CD切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.
如图,AB是⊙O的直径,AM和BN是它的两条切线,CD切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.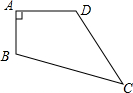 如图四边形ABCD,已知∠A=90°,AB=3,BC=13,CD=12,DA=4.求四边形的面积.
如图四边形ABCD,已知∠A=90°,AB=3,BC=13,CD=12,DA=4.求四边形的面积.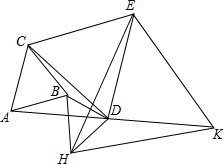 如图,位于同一平面内的正△ABC、正△CDE和正△EHK(顶点依逆时针方向排列),两两地有公共点C和E,且D是AK的中点,求证:△BHD也是正三角形.
如图,位于同一平面内的正△ABC、正△CDE和正△EHK(顶点依逆时针方向排列),两两地有公共点C和E,且D是AK的中点,求证:△BHD也是正三角形.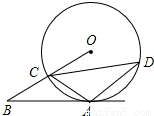 如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,且C为OB的中点,过C点作弦CD,若∠ACD=45°,AD=2.求AC的长.
如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,且C为OB的中点,过C点作弦CD,若∠ACD=45°,AD=2.求AC的长.