题目内容
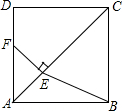 如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.(1)求证:DF=AE;
(2)当AB=2时,求BE2的值.
考点:正方形的性质,角平分线的性质,勾股定理
专题:
分析:(1)连接CF,根据“HL”证明Rt△CDF和Rt△CEF全等,根据全等三角形对应边相等可得DF=EF,根据正方形的对角线平分一组对角可得∠EAF=45°,求出△AEF是等腰直角三角形,再根据等腰直角三角形的性质可得AE=EF,然后等量代换即可得证;
(2)根据正方形的对角线等于边长的
倍求出AC,然后求出AE,过点E作EH⊥AB于H,判断出△AEH是等腰直角三角形,然后求出EH=AH=
AE,再求出BH,然后利用勾股定理列式计算即可得解.
(2)根据正方形的对角线等于边长的
| 2 |
| ||
| 2 |
解答:(1)证明:如图,连接CF,
在Rt△CDF和Rt△CEF中,
,
∴Rt△CDF≌Rt△CEF(HL),
∴DF=EF,
∵AC是正方形ABCD的对角线,
∴∠EAF=45°,
∴△AEF是等腰直角三角形,
∴AE=EF,
∴DF=AE;
(2)解:∵AB=2,
∴AC=
AB=2
,
∵CE=CD,
∴AE=2
-2,
过点E作EH⊥AB于H,
则△AEH是等腰直角三角形,
∴EH=AH=
AE=
×(2
-2)=2-
,
∴BH=2-(2-
)=
,
在Rt△BEH中,BE2=BH2+EH2=(
)2+(2-
)2=8-4
.
在Rt△CDF和Rt△CEF中,
|
∴Rt△CDF≌Rt△CEF(HL),
∴DF=EF,
∵AC是正方形ABCD的对角线,
∴∠EAF=45°,

∴△AEF是等腰直角三角形,
∴AE=EF,
∴DF=AE;
(2)解:∵AB=2,
∴AC=
| 2 |
| 2 |
∵CE=CD,
∴AE=2
| 2 |
过点E作EH⊥AB于H,
则△AEH是等腰直角三角形,
∴EH=AH=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
∴BH=2-(2-
| 2 |
| 2 |
在Rt△BEH中,BE2=BH2+EH2=(
| 2 |
| 2 |
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,勾股定理的应用,作辅助线构造出全等三角形和直角三角形是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,∠C=60°,∠A=50°,AB的垂直平分线交AC于D,则∠DBC=( )
如图,∠C=60°,∠A=50°,AB的垂直平分线交AC于D,则∠DBC=( )| A、5° | B、10° |
| C、20° | D、30° |
不等式2x+5>0的解集是( )
A、x<
| ||
B、x>
| ||
C、x>-
| ||
D、x<-
|
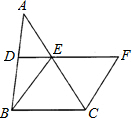 如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.