题目内容
解不等式及分式方程:
(1)5(x+2)≥1-2(x-1);
(2)
;
(3)
+
=3.
(1)5(x+2)≥1-2(x-1);
(2)
|
(3)
| 3 |
| 2x-2 |
| 1 |
| 1-x |
考点:解一元一次不等式组,解分式方程,解一元一次不等式
专题:
分析:(1)去括号、去分母、移项、合并同类项,系数化成1即可求解;
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集;
(3)去括号、去分母、移项、合并同类项,系数化成1即可求得x的值,然后进行检验即可.
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集;
(3)去括号、去分母、移项、合并同类项,系数化成1即可求得x的值,然后进行检验即可.
解答:解:(1)去括号,得:5x+10≥1-2x+2,
移项,得:5x+2x≥1+2-10,
合并同类项,得:7x≥-7,
系数化成1得:x≥-1;
(2)
,
解①得:y<8,
解②得:y≥2,
则不等式组的解集是:2≤y<8;
(3)去分母,得:3-2=3(2x-2),
去括号,得:1=6x-6,
移项,合并同类项,得:7=6x,
系数化成1得:x=
.
检验:当x=
时,2x-2=
≠0,
则方程的解是:x=
.
移项,得:5x+2x≥1+2-10,
合并同类项,得:7x≥-7,
系数化成1得:x≥-1;
(2)
|
解①得:y<8,
解②得:y≥2,
则不等式组的解集是:2≤y<8;
(3)去分母,得:3-2=3(2x-2),
去括号,得:1=6x-6,
移项,合并同类项,得:7=6x,
系数化成1得:x=
| 7 |
| 6 |
检验:当x=
| 7 |
| 6 |
| 1 |
| 3 |
则方程的解是:x=
| 7 |
| 6 |
点评:本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
相关题目
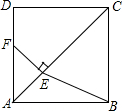 如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.