题目内容
8.△ABC中,AB=5,AC=3,AD是△ABC的中线,设AD长为m,则m的取值范围是1<m<4.分析 作辅助线,构建△AEC,根据三角形三边关系得:EC-AC<AE<AC+EC,即5-3<2m<5+3,所以1<m<4.
解答 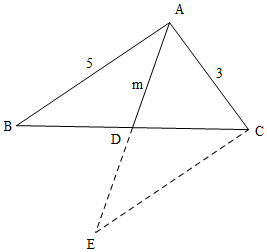 解:延长AD至E,使AD=DE,连接CE,则AE=2m,
解:延长AD至E,使AD=DE,连接CE,则AE=2m,
∵AD是△ABC的中线,
∴BD=CD,
在△ADB和△EDC中,
∵$\left\{\begin{array}{l}{AD=DE}\\{∠ADB=∠EDC}\\{BD=CD}\end{array}\right.$,
∴△ADB≌△EDC,
∴EC=AB=5,
在△AEC中,EC-AC<AE<AC+EC,
即5-3<2m<5+3,
∴1<m<4,
故答案为:1<m<4.
点评 本题考查了三角形三边关系、三角形全等的性质和判定,属于基础题,辅助线的作法是关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
16.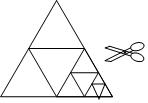 如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( )
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( )
 如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( )
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( )| A. | 332 | B. | 333 | C. | 334 | D. | 335 |
13.中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第六天走的路程为( )
| A. | 24里 | B. | 12里 | C. | 6里 | D. | 3里 |
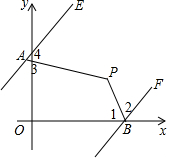
20.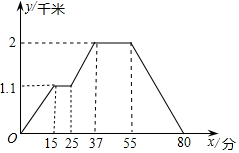 如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )
如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )
 如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )
如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )| A. | 1.1千米 | B. | 2千米 | C. | 15千米 | D. | 37千米 |
17.下列计算错误的是( )
| A. | $(\frac{1}{2})^{-2}$=4 | B. | 32×3-1=3 | ||
| C. | 20÷2-2=$\frac{1}{4}$ | D. | (-3×102)3=-2.7×107 |
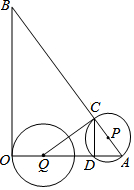 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.