题目内容
11.(1)如图1,在等腰△ABC中,AB=AC,E、D是AB、AC上的点,且BE=CD,∠BEC+∠BDC=180°,求证:∠1=∠2=$\frac{1}{2}$∠A.(2)如图2,若将(1)中等腰△ABC改为非等腰△ABC(即AB≠AC),其余条件不变,试问∠1=∠2=$\frac{1}{2}$∠A是否仍然成立,若成立,请加以证明;若不成立.请说明理由.
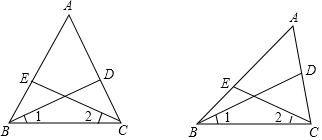
分析 (1)先判断出,△BCD≌△CBE,得出∠1=∠2,∠BDC=∠CEB,再用同角的余角相等即可得出结论;
(2)先构造出,△BEM≌△CDN,得出BM=CN,进而判断出Rt△BCM≌Rt△CBN,最后用三角形和四边形的内角和即可得出结论.
解答 解:(1)∵AB=AC,
∴∠ABC=∠ACB,
在△BCD和△CBE中,$\left\{\begin{array}{l}{CD=BE}\\{∠ACB=∠ABC}\\{BC=CB}\end{array}\right.$,
∴△BCD≌△CBE,
∴∠1=∠2,∠BDC=∠CEB,
∵∠BEC+∠BDC=180°,
∴∠BDC=∠CEB=90°,
∴∠1+∠BCD=90°,
∵∠A+2∠BCD=180°,
∴$\frac{1}{2}$∠A+∠BCD=90°,
∴∠1=$\frac{1}{2}$∠A,
即:∠1=∠2=$\frac{1}{2}$∠A;
(2)∠1=∠2=$\frac{1}{2}$∠A是仍然成立,
理由:如图,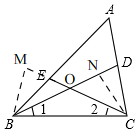
过点B作BM⊥CE,过点C作CN⊥BD,
∵∠BEC+∠BDC=180°,∠BEC+∠BEM=180°,
∴∠BEM=∠CDN,
在△BEM和△CDN中,$\left\{\begin{array}{l}{∠BME=∠CND=90°}\\{∠BEM=∠CDN}\\{BE=CD}\end{array}\right.$,
∴△BEM≌△CDN,
∴BM=CN,
在Rt△BCM和Rt△CBN中,$\left\{\begin{array}{l}{BM=CN}\\{BC=CB}\end{array}\right.$,
∴Rt△BCM≌Rt△CBN,
∴∠1=∠2,
在△BOC中,2∠1+∠BOC=180°,
在四边形AEOD中,∵∠AEO+∠ADO=180°,
∴∠A+∠DOE=180°,
∵∠DOE=∠BOC,
∴∠2∠1=∠A,
∴∠1=$\frac{1}{2}$∠A,
即:∠1=∠2=$\frac{1}{2}$∠A.
点评 此题是等腰三角形的性质,主要考查了全等三角形的判定和性质,三角形的内角和,四边形的内角和,同角(或等角)的余角(或补角)相等,解本题的关键是得出∠1=∠2,构造出△BEM≌△CDN是解本题的难点.

| A. |  | B. |  | C. |  | D. |  |
 如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O在BD上,过O点作OE⊥BC于E,OF⊥AC于F,OE=OF.
如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O在BD上,过O点作OE⊥BC于E,OF⊥AC于F,OE=OF.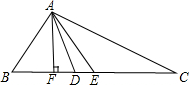 如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则:
如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则: 如图,BC是⊙O的一个内接正五边形的一边,请用等分圆周的方法,在⊙A中用尺规作图作出一个⊙A的内接正五边形(请保留作图痕迹).
如图,BC是⊙O的一个内接正五边形的一边,请用等分圆周的方法,在⊙A中用尺规作图作出一个⊙A的内接正五边形(请保留作图痕迹). 在下面的四个三角形中,不能由如图的三角形经过旋转或平移得到的是( )
在下面的四个三角形中,不能由如图的三角形经过旋转或平移得到的是( )

