题目内容
2.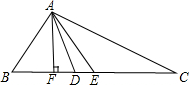 如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则:
如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则:(1)∵AE是△ABC的中线,
∴BE=CE=$\frac{1}{2}$BC;
(2)∵AD是△ABC的角平分线,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC;
(3)∵AF是△ABC的高,
∴∠AFB=∠AFC=90°;
(4)∵AE是△ABC的中线,
∴BE=CE,
又∵S△ABE=$\frac{1}{2}$S△ABC,S△AEC=$\frac{1}{2}$S△ABC,
∴S△ABE=S△ACE=$\frac{1}{2}$S△ABC.
分析 (1)三角形一边的中点与此边所对顶点的连线叫做三角形的中线;
(2)三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线;
(3)从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高;
(4)三角形的中线将三角形分成面积相等的两部分.
解答 解:(1)根据AE是△ABC的中线,可得BE=CE=$\frac{1}{2}$ BC;
(2)根据AD是△ABC的角平分线,可得∠BAD=∠CAD=$\frac{1}{2}$∠BAC;
(3)根据AF是△ABC的高,可得∠AFB=∠AFC=90°;
(4)根据AE是△ABC的中线,可得BE=CE,所以S△ABE=$\frac{1}{2}$S△ABC,S△AEC=$\frac{1}{2}$S△ABC,即S△ABE=S△ACE=$\frac{1}{2}$S△ABC.
故答案为:(1)CE,BC;(2)∠CAD,∠BAC;(3)∠AFC;(4)S△ABC,S△ABC,S△ABC.
点评 本题主要考查了三角形的中线、高线以及角平分线的概念的运用,解题时注意:三角形有三条中线,有三条高线,有三条角平分线,它们都是线段,三角形的中线将三角形分成面积相等的两部分.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.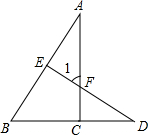 如图所示,AC⊥BD于点C,DE⊥AB于点E.
如图所示,AC⊥BD于点C,DE⊥AB于点E.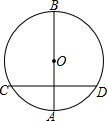 如图,AB是⊙O的直径,弦CD垂直平分OA,求劣弧CD所对的圆周角的度数.
如图,AB是⊙O的直径,弦CD垂直平分OA,求劣弧CD所对的圆周角的度数.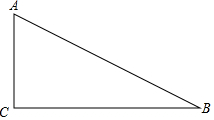 如图Rt△ABC,作一个圆,使圆心O在AC上,且与AB、BC所在直线相切,并说明作图理由.
如图Rt△ABC,作一个圆,使圆心O在AC上,且与AB、BC所在直线相切,并说明作图理由.