题目内容
15.函数的图象过(0,-3),(-2,-1)两点(1)求这个一次函数的解析式.
(2)判断点(2,-3),点(4,-7)是否在一次函数的图象上?
分析 (1)设一次函数解析式为y=kx+b,把(0,-3),(-2,-1)得到关于k、b的方程组,然后解方程组求出k、b即可得到一次函数解析式;
(2)根据一次函数图象上点的坐标特征进行判断.
解答 解:(1)设一次函数解析式为y=kx+b,
把(0,-3),(-2,-1)代入得$\left\{\begin{array}{l}{b=-3}\\{-2k+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=-3}\end{array}\right.$,
所以一次函数解析式为y=-x-3;
(2)当x=2时,y=-x-3=-5,所以点(2,-3)不在直线y=-x-3上;
当x=4时,y=-x-3=-7,所以点(4,-7)在直线y=-x-3上.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.也考查了一次函数图象上点的坐标特征.

练习册系列答案
相关题目
20.已知直角三角形的两条直角边的长分别为$\sqrt{3}$和$\sqrt{6}$,则这个直角三角形的面积为( )
| A. | $\sqrt{18}$ | B. | 2$\sqrt{18}$ | C. | $\frac{3}{2}$$\sqrt{2}$ | D. | 18 |
7.$\sqrt{(-4)^{2}}$的平方根是( )
| A. | ±4 | B. | 4 | C. | ±2 | D. | 2 |
5.下列变形正确的是( )
| A. | (a2)3=a9 | B. | 2a×3a=6a2 | C. | a6-a2=a4 | D. | 2a+3b=6ab |
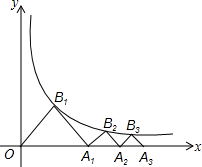 已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12.
已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12.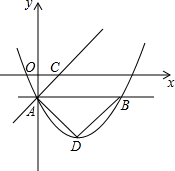 如图,抛物线y=ax2+bx-1(a≠0)的对称轴是直线x=2,最低点D的纵坐标为-3,A,B为抛物线上的两点,且直线AB∥x轴.
如图,抛物线y=ax2+bx-1(a≠0)的对称轴是直线x=2,最低点D的纵坐标为-3,A,B为抛物线上的两点,且直线AB∥x轴.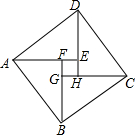 如图,由四个全等的直角三角形拼成“赵爽弦图”. Rt△ABF中,∠AFB=90°,AF=3,AB=5.四边形EFGH的面积是1.
如图,由四个全等的直角三角形拼成“赵爽弦图”. Rt△ABF中,∠AFB=90°,AF=3,AB=5.四边形EFGH的面积是1.