题目内容
6.当x≥$\frac{2}{3}$时,式子$\frac{3x-2}{-5}$的值是非正数.分析 根据题意可得$\frac{3x-2}{-5}$≤0,解x的一元一次不等式,即可求出x的取值范围.
解答 解:依题意得$\frac{3x-2}{-5}$≤0,
即3x-2≥0,
解得x≥$\frac{2}{3}$.
故答案为x≥$\frac{2}{3}$.
点评 本题考查了解一元一次不等式,列出关于x不等式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.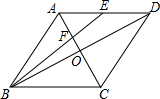 如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )
如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )
 如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )
如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
11.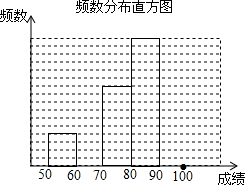 一所中学,为了让学生了解环保知识,增强环保意识,举行了一次环保知识竞赛,共有900名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(得分均为正整数,满分100分)进行统计.
一所中学,为了让学生了解环保知识,增强环保意识,举行了一次环保知识竞赛,共有900名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(得分均为正整数,满分100分)进行统计.
请根据表和图,解答下列问题:
(1)频率分布表中的m=12;n=0.24.
(2)补全频数分布直方图;
(3)全体参赛学生中,竞赛成绩的中位数落在哪个组内?直接填空80.5~90.5.
(4)若成绩在90分以上(不含90分)可以获奖,在全校学生的试卷中任抽取一张,获奖的概率是24%.
 一所中学,为了让学生了解环保知识,增强环保意识,举行了一次环保知识竞赛,共有900名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(得分均为正整数,满分100分)进行统计.
一所中学,为了让学生了解环保知识,增强环保意识,举行了一次环保知识竞赛,共有900名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(得分均为正整数,满分100分)进行统计.请根据表和图,解答下列问题:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100 | m | n |
| 合计 |
(2)补全频数分布直方图;
(3)全体参赛学生中,竞赛成绩的中位数落在哪个组内?直接填空80.5~90.5.
(4)若成绩在90分以上(不含90分)可以获奖,在全校学生的试卷中任抽取一张,获奖的概率是24%.
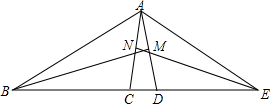 如图,已知点B,C,D,E在同一条直线上,BM,EN分别垂直平分AD,AC于M,N.
如图,已知点B,C,D,E在同一条直线上,BM,EN分别垂直平分AD,AC于M,N.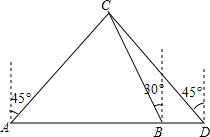 某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值) 如图:矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,试判断四边形CODP的形状.
如图:矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,试判断四边形CODP的形状.