题目内容
17.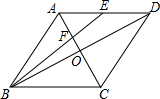 如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )
如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
分析 由四边形ABCD是菱形,于是得到AD=BC,AD∥BC,AO=CO,证得△AEF∽△CFB,得到$\frac{AF}{CF}=\frac{AE}{BC}$,证得$\frac{AF}{CF}=\frac{1}{2}$,推出$\frac{AF}{AC}=\frac{1}{3}$,得到$\frac{AF}{AO}=\frac{2}{3}$,即可得到结论.
解答 解:∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,AO=CO,
∴△AEF∽△CFB,
∴$\frac{AF}{CF}=\frac{AE}{BC}$,
∵AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴$\frac{AF}{CF}=\frac{1}{2}$,
∴$\frac{AF}{AC}=\frac{1}{3}$,
∴AC=3AF,
∵AC=2AO,
∴$\frac{AF}{AO}=\frac{2}{3}$,
∴OF=$\frac{1}{3}$AO,
∴$\frac{AF}{OF}$=2.
故选D.
点评 本题考查了相似三角形的判定和性质,菱形的性质,熟练掌握相似三角形的判定定理是解题的关键.

练习册系列答案
相关题目
12. 如图,DE∥BC,∠ADE=70°,则∠ABC的度数为( )
如图,DE∥BC,∠ADE=70°,则∠ABC的度数为( )
 如图,DE∥BC,∠ADE=70°,则∠ABC的度数为( )
如图,DE∥BC,∠ADE=70°,则∠ABC的度数为( )| A. | 70° | B. | 60° | C. | 110° | D. | 50° |
9.若点(-1,2)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点一定在该图象上的是( )
| A. | (-2,-1) | B. | (-$\frac{1}{2}$,2) | C. | (2,-1) | D. | ($\frac{1}{2}$,2) |
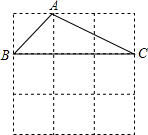 如图,△ABC的三个顶点分别在格子的3个交点上,请你试着再在格子的交点上找出三个点D,E,F,使得△DEF≌△ABC.
如图,△ABC的三个顶点分别在格子的3个交点上,请你试着再在格子的交点上找出三个点D,E,F,使得△DEF≌△ABC.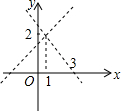 如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$. 同桌读了:“子非鱼焉知鱼之乐乎?”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问:由图中所示的图案通过平移后得到的图案是( )
同桌读了:“子非鱼焉知鱼之乐乎?”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问:由图中所示的图案通过平移后得到的图案是( )



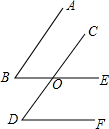 已知:如图,AB∥CD,∠B=∠D,求证:BE∥DF.
已知:如图,AB∥CD,∠B=∠D,求证:BE∥DF.