题目内容
15. 如图:矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,试判断四边形CODP的形状.
如图:矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,试判断四边形CODP的形状.
分析 根据一组对边平行且相等的四边形是平行四边形可得四边形CODP是平行四边形,再根据矩形的对角线互相平分且相等可得OC=OD,然后根据邻边相等的平行四边形是菱形解答.
解答 解:四边形CODP是菱形,
理由:∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵矩形ABCD的对角线AC、BD交于点O,
∴OC=OD,
∴平行四边形CODP是菱形,
故四边形CODP是菱形.
点评 本题考查了矩形的性质,菱形的判定,关键是掌握矩形对角线互相平分且相等,邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
4.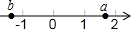 已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )
已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )
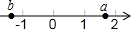 已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )
已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )| A. | 2a+2b | B. | 2b+3 | C. | 2a-3 | D. | -1 |
 同桌读了:“子非鱼焉知鱼之乐乎?”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问:由图中所示的图案通过平移后得到的图案是( )
同桌读了:“子非鱼焉知鱼之乐乎?”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问:由图中所示的图案通过平移后得到的图案是( )



 y=kx+b(k≠0)的图象如图所示,当y<0时,x的取值范围是x>1.
y=kx+b(k≠0)的图象如图所示,当y<0时,x的取值范围是x>1.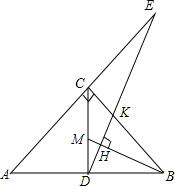 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证:
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证: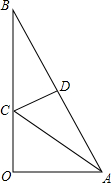 如图,直角三角形纸片OAB,∠AOB=90°,OA=1,OB=2,折叠该纸片,折痕与边OB交于点C,与边AB交于点D,折叠后点B与点A重合.
如图,直角三角形纸片OAB,∠AOB=90°,OA=1,OB=2,折叠该纸片,折痕与边OB交于点C,与边AB交于点D,折叠后点B与点A重合.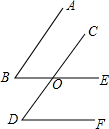 已知:如图,AB∥CD,∠B=∠D,求证:BE∥DF.
已知:如图,AB∥CD,∠B=∠D,求证:BE∥DF.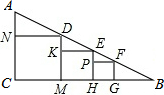 如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.
如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.