题目内容
16.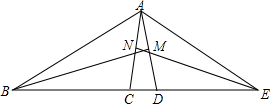 如图,已知点B,C,D,E在同一条直线上,BM,EN分别垂直平分AD,AC于M,N.
如图,已知点B,C,D,E在同一条直线上,BM,EN分别垂直平分AD,AC于M,N.(1)当∠CAD=30°时,请你求出∠BAE的度数.
(2)当∠CAD=45°时,∠BAE=90°,请证明你的结论.
分析 (1)根据线段垂直平分线求出AB=BD,AE=CE,根据等腰三角形的性质求出∠BAD=∠ADB,∠EAC=∠ACE,根据三角形内角和定理求出∠DAB+∠CAE,即可求出答案;
(2)根据线段垂直平分线求出AB=BD,AE=CE,根据等腰三角形的性质求出∠BAD=∠ADB,∠EAC=∠ACE,根据三角形内角和定理求出∠DAB+∠CAE,即可求出答案.
解答 解:(1)∵BM,EN分别垂直平分AD,AC于M,N,
∴AB=BD,AE=CE,
∴∠BAD=∠ADB,∠EAC=∠ACE,
∵∠CAD=30°,
∴∠DAB+∠CAE=∠ADB+∠ACE=180°-∠CAD=150°,
∴∠BAE=∠DAB+∠CAE-∠CAD=150°-30°=120°;
(2)当∠CAD=45°时,∠BAE=90°,
证明:∵BM,EN分别垂直平分AD,AC于M,N,
∴AB=BD,AE=CE,
∴∠BAD=∠ADB,∠EAC=∠ACE,
∵∠CAD=45°,
∴∠DAB+∠CAE=∠ADB+∠ACE=180°-∠CAD=135°,
∴∠BAE=∠DAB+∠CAE-∠CAD=135°-45°=90°,
即当∠CAD=45°时,∠BAE=90°,
故答案为:45°.
点评 本题考查了线段垂直平分线性质,等腰三角形的性质,三角形的内角和定理的应用,能灵活运用定理进行推理和计算是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
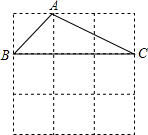 如图,△ABC的三个顶点分别在格子的3个交点上,请你试着再在格子的交点上找出三个点D,E,F,使得△DEF≌△ABC.
如图,△ABC的三个顶点分别在格子的3个交点上,请你试着再在格子的交点上找出三个点D,E,F,使得△DEF≌△ABC.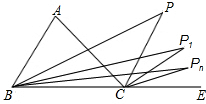 已知BP1平分∠ABC,CP1平分∠ACD;BP2平分∠P1BC,CP2平分∠P1CD;…,如此下去,得到∠Pn和∠A关系为∠Pn=($\frac{1}{2}$)n∠A.
已知BP1平分∠ABC,CP1平分∠ACD;BP2平分∠P1BC,CP2平分∠P1CD;…,如此下去,得到∠Pn和∠A关系为∠Pn=($\frac{1}{2}$)n∠A.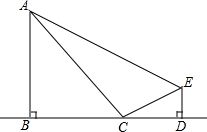 如图,分别过点A、E作AB⊥BD,ED⊥BD,C为线段BD上一动点,连接AC、EC.已知AB=9,DE=1,AE=17,设CD=x,用含x的代数式表示AC+CE.
如图,分别过点A、E作AB⊥BD,ED⊥BD,C为线段BD上一动点,连接AC、EC.已知AB=9,DE=1,AE=17,设CD=x,用含x的代数式表示AC+CE.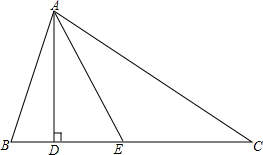 如图,△ABC中,∠B>∠C,AD是高,AE平分∠BAC,求证:∠DAE=$\frac{1}{2}$(∠B-∠C).
如图,△ABC中,∠B>∠C,AD是高,AE平分∠BAC,求证:∠DAE=$\frac{1}{2}$(∠B-∠C).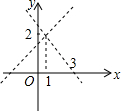 如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$. 同桌读了:“子非鱼焉知鱼之乐乎?”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问:由图中所示的图案通过平移后得到的图案是( )
同桌读了:“子非鱼焉知鱼之乐乎?”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问:由图中所示的图案通过平移后得到的图案是( )


