题目内容
 如图,将△ABC绕点A逆时针方向旋转到△ADE的位置,点B落在AC边上的点D处,设旋转角为α (0°<α<90°).若∠B=125°,∠E=30°,则∠α=
如图,将△ABC绕点A逆时针方向旋转到△ADE的位置,点B落在AC边上的点D处,设旋转角为α (0°<α<90°).若∠B=125°,∠E=30°,则∠α=考点:旋转的性质
专题:计算题
分析:根据旋转的性质得∠C=∠E=30°,∠DAB=α,然后根据三角形内角和定理计算出∠CAB=25°,从而得到∠α=25°.
解答:解:∵△ABC绕点A逆时针方向旋转到△ADE的位置,点B落在AC边上的点D处,
∴∠C=∠E=30°,∠DAB=α,
∵∠CAB+∠C+∠B=180°,
∴∠CAB=180°-30°-125°=25°,
∴∠α=25°.
故答案为25.
∴∠C=∠E=30°,∠DAB=α,
∵∠CAB+∠C+∠B=180°,
∴∠CAB=180°-30°-125°=25°,
∴∠α=25°.
故答案为25.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.

练习册系列答案
相关题目
关于数据-4,1,2,-1,2,下面结果中,错误的是( )
| A、中位数为1 | B、平均数为0 |
| C、众数为2 | D、方差为26 |
 如图,已知在?ABCD中,对角线AC、BD相交于点O,AE⊥BD,BM⊥AC、DN⊥AC,CF⊥BD垂足分别是E、M、N、F,求证:EN∥MF.
如图,已知在?ABCD中,对角线AC、BD相交于点O,AE⊥BD,BM⊥AC、DN⊥AC,CF⊥BD垂足分别是E、M、N、F,求证:EN∥MF.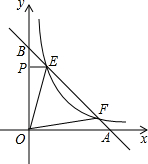 如图,点E,F在函数y=
如图,点E,F在函数y= 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是