题目内容
 如图,已知在?ABCD中,对角线AC、BD相交于点O,AE⊥BD,BM⊥AC、DN⊥AC,CF⊥BD垂足分别是E、M、N、F,求证:EN∥MF.
如图,已知在?ABCD中,对角线AC、BD相交于点O,AE⊥BD,BM⊥AC、DN⊥AC,CF⊥BD垂足分别是E、M、N、F,求证:EN∥MF.考点:平行四边形的判定与性质
专题:证明题
分析:连接ME,FN,由四边形ABCD为平行四边形,得到对角线互相平分,利用AAS得到三角形AOE与三角形COF全等,利用全等三角形对应边相等得到OE=OF,同理得到三角形BOM与三角形DON全等,得到OM=ON,进而确定出四边形MEFN为平行四边形,利用平行四边形的对边平行即可得证.
解答: 证明:连接ME,FN,
证明:连接ME,FN,
∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD,
∵AE⊥BD,CF⊥BD,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴OE=OF,
同理△BOM≌△DON,得到OM=ON,
∴四边形EMFN为平行四边形,
∴EN∥MF.
 证明:连接ME,FN,
证明:连接ME,FN,∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD,
∵AE⊥BD,CF⊥BD,
在△AOE和△COF中,
|
∴△AOE≌△COF(AAS),
∴OE=OF,
同理△BOM≌△DON,得到OM=ON,
∴四边形EMFN为平行四边形,
∴EN∥MF.
点评:此题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.

练习册系列答案
相关题目
一次函数y=kx+b的图象经过点(m2+1,1)和(-1,m2+1)(m≠0),则k、b应满足的条件是( )
| A、k>0,b>0 |
| B、k>0,b<0 |
| C、k<0,b<0 |
| D、k<0,b>0 |
 如图,将△ABC绕点A逆时针方向旋转到△ADE的位置,点B落在AC边上的点D处,设旋转角为α (0°<α<90°).若∠B=125°,∠E=30°,则∠α=
如图,将△ABC绕点A逆时针方向旋转到△ADE的位置,点B落在AC边上的点D处,设旋转角为α (0°<α<90°).若∠B=125°,∠E=30°,则∠α=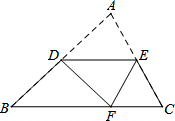 如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=42°,则∠BDF的度数为
如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=42°,则∠BDF的度数为