Question

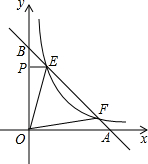如图，点E，F在函数y=

k

x

（x＞0）的图象上，直线EF分别与x轴、y轴交于点A，B，且BE：BF=1：m．过点E作EP⊥y轴于P，已知△OEP的面积为1，则k值是

 

，△OEF的面积是

 

（用含m的式子表示）

Answer 1

考点：反比例函数综合题

专题：综合题

分析：作EC⊥x轴于C，FD⊥x轴于D，FH⊥y轴于H，根据反比例函数的比例系数的几何意义由△OEP的面积为1易得k=2，则反比例函数解析式为y=

2

x

，再证明△BPE∽△BHF，利用相似比可得HF=mPE，根据反比例函数图象上点的坐标特征，设E点坐标为（t，

2

t

），则F点的坐标为（tm，

2

tm

），由于S_△OEF+S_△OFD=S_△OEC+S_梯形ECDF，S_△OFD=S_△OEC=1，所以S_△OEF=S_梯形ECDF，然后根据梯形面积公式计算．

解答：解：作EC⊥x轴于C，FD⊥x轴于D，FH⊥y轴于H，如图，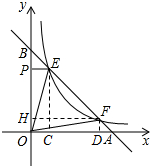
∵△OEP的面积为1，
∴

1

2

|k|=1，
而k＞0，
∴k=2，
∴反比例函数解析式为y=

2

x

，
∵EP⊥y轴，FH⊥y轴，
∴EP∥FH，
∴△BPE∽△BHF，
∴

PE

HF

=

BE

BF

=

1

m

，即HF=mPE，
设E点坐标为（t，

2

t

），则F点的坐标为（tm，

2

tm

），
∵S_△OEF+S_△OFD=S_△OEC+S_梯形ECDF，
而S_△OFD=S_△OEC=1，
∴S_△OEF=S_梯形ECDF=

1

2

（

2

tm

+

2

t

）（tm-t）
=（

1

m

+1）（m-1）
=

m2-1

m

．
故答案为：2，

m2-1

m

．

点评：本题考查了反比例函数的综合题：掌握反比例函数图象上点的坐标特征、反比例函数的比例系数的几何意义；会利用相似比确定线段之间的关系．