题目内容
1.(1)计算:($\frac{1}{4}$)-1-$\sqrt{27}$+(5-π)0(2)先化简再求值:$(\frac{1}{x+2}-1)÷\frac{{{x^2}+2x+1}}{{{x^2}-4}}$,其中x=tan60°-1.
分析 (1)首先计算乘方、开方,然后进行加减即可;
(2)先对括号内的式子进行通分相减,把除法转化为乘法,然后计算乘法即可化简,然后化简x的值,代入计算即可..
解答 解:(1)原式=4-3$\sqrt{3}$+1=3-3$\sqrt{3}$;
(2)原式=$\frac{1-(x+2)}{x+2}$•$\frac{(x+2)(x-2)}{(x+1)^{2}}$=-$\frac{x+1}{x+2}$•$\frac{(x+2)(x-2)}{(x+1)^{2}}$=-$\frac{x-2}{x+1}$,
当x=tan60°-1=$\sqrt{3}$-1时,原式=$\frac{\sqrt{3}-1-2}{\sqrt{3}-1+1}$=$\frac{\sqrt{3}-3}{\sqrt{3}}$=1-$\sqrt{3}$.
点评 本题考查了分时的化简求值,正确对分式的分母、分子进行分解因式是关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,矩形OABC的顶点O为原点,E为AB上一点,把△CBE沿CE折叠,使点B恰好落在OA边上的点D处,A、D的坐标分别为(5,0)和(3,0).
如图,在平面直角坐标系中,矩形OABC的顶点O为原点,E为AB上一点,把△CBE沿CE折叠,使点B恰好落在OA边上的点D处,A、D的坐标分别为(5,0)和(3,0).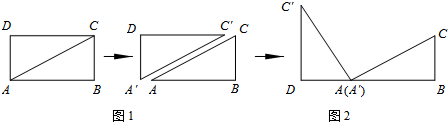
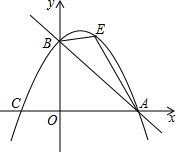 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.抛物线y=ax2+$\frac{3}{4}x+c$经过A、B两点,点E是直线AB上方抛物线上的一点.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.抛物线y=ax2+$\frac{3}{4}x+c$经过A、B两点,点E是直线AB上方抛物线上的一点.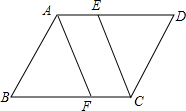 如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明:
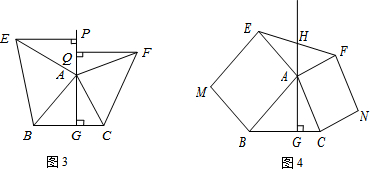
如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明: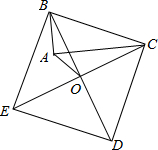 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.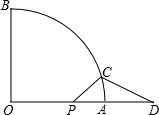 如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.
如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.