题目内容
16.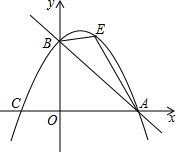 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.抛物线y=ax2+$\frac{3}{4}x+c$经过A、B两点,点E是直线AB上方抛物线上的一点.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.抛物线y=ax2+$\frac{3}{4}x+c$经过A、B两点,点E是直线AB上方抛物线上的一点.(1)求抛物线所对应的函数表达式.
(2)求△ABE面积的最大值,并求出此时点E的坐标.
(3)在(2)的前提下,过点E作y轴的平行线交直线AB于点M,连结CM.点Q在抛物线对称轴上,点P在抛物线上.当以P、Q、C、M为顶点的四边形是平行四边形时,请直接写出点P的坐标.
分析 (1)由直线AB的解析式可求出点A、B的坐标,将A、B的坐标代入抛物线解析式即可得出关于a、c的二元一次方程,解方程即可得出结论;
(2)过点E作EF⊥x轴于点F交直线AB与点M,设点E的坐标为(m,-$\frac{3}{8}{m}^{2}+\frac{3}{4}$m+3),点M的坐标为(m,-$\frac{3}{4}$m+3),根据S△ABE=S△BEM+S△AEM即可得出S关于m的函数解析式,根据二次函数的性质即可解决最值问题;
(3)根据(2)的结论可求出点M的坐标,设点P的坐标为(n,-$\frac{3}{8}{n}^{2}+\frac{3}{4}$n+3),Q点的坐标为(1,d),以P、Q、C、M为顶点的四边形是平行四边形分两种情况:①CM为对角线,根据中点坐标公式即可得出n的一元一次方程,解方程即可得出P点的坐标;②CM为一条边,根据平行四边形的性质可依据PQ的横坐标之差等于CM的横坐标之差找出关于n的一元一次方程,解方程即可得出n值,由n值即可解决问题.
解答 解:(1)当x=0时,y=3,
即B点的坐标为(0,3),
当y=0时,有-$\frac{3}{4}$x+3=0,
解得x=4,即A点坐标为(4,0).
将A、B点坐标代入抛物线的解析式,
得$\left\{\begin{array}{l}{16a+3+c=0}\\{c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{3}{8}}\\{c=3}\end{array}\right.$,
故抛物线所对应的函数表达式为y=-$\frac{3}{8}{x}^{2}+\frac{3}{4}$x+3.
(2)过点E作EF⊥x轴于点F交直线AB与点M,如图1所示.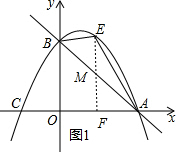
∵点E是直线AB上方抛物线上的点,
∴设点E的坐标为(m,-$\frac{3}{8}{m}^{2}+\frac{3}{4}$m+3),点M的坐标为(m,-$\frac{3}{4}$m+3),
∴EM=-$\frac{3}{8}{m}^{2}+\frac{3}{4}$m+3-(-$\frac{3}{4}$m+3)=-$\frac{3}{8}{m}^{2}+\frac{3}{2}$m,
∴S△ABE=S△BEM+S△AEM=$\frac{1}{2}$ME•OA=$\frac{1}{2}$×(-$\frac{3}{8}{m}^{2}+\frac{3}{2}$m)×4=-$\frac{3}{4}{m}^{2}$+3m=-$\frac{3}{4}$(m-2)2+3,
∴当m=2时,△ABE面积最大,且最大值为3,此时点E的坐标为(2,3).
(3)抛物线的对称轴为x=-$\frac{\frac{3}{4}}{2×(-\frac{3}{8})}$=1.
设点P的坐标为(n,-$\frac{3}{8}{n}^{2}+\frac{3}{4}$n+3),Q点的坐标为(1,d).
∵点E的坐标为(2,3),
∴直线EM的解析式为x=2,
∴点M的坐标为(2,$\frac{3}{2}$).
∵令y=0,则有-$\frac{3}{8}{x}^{2}+\frac{3}{4}$x+3=0,解得x=-2,或x=4,
∴点C的坐标为(-2,0),
当以P、Q、C、M为顶点的四边形是平行四边形时,分两种情况:
①如图2所示,线段CM为对角线,且CM的中点为点N.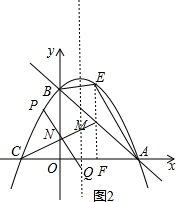
∵点C(-2,0),点M(2,$\frac{3}{2}$),
∴点N的坐标为(0,$\frac{3}{4}$).
又∵点N为线段PQ的中点,
∴有$\frac{n+1}{2}$=0,解得n=-1,
此时P点的坐标为(-1,$\frac{15}{8}$);
②线段CM为一条边时,PQ的横坐标之差等于CM的横坐标之差,
即|1-n|=|2-(-2)|,
解得:n=-3或n=5,
此时点P的坐标为(-3,-$\frac{21}{8}$)或(5,-$\frac{21}{8}$).
综上可知:点P的坐标为(-3,-$\frac{21}{8}$),(5,-$\frac{21}{8}$)和(-1,$\frac{15}{8}$).
点评 本题考查了待定系数法求函数解析式、二次函数的性质、中点坐标公式、平行四边形的性质以及解一元一次方程,解题的关键:(1)待定系数法求函数解析式;(2)利用三角形的面积公式找出S关于m的函数关系式;(3)分两种情况考虑.本题属于中档题,(1)难度不大;(2)借助了二次函数的性质来解决最值问题,有点难度;(3)巧妙利用平行四边形的性质,找出关于n的一次方程,此问难度不小,易失分.

| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
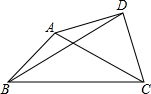 如图四边形ABCD中,AB=4$\sqrt{2}$,BC=12,∠ABC=45°,∠ADC=90°,AD=CD,则BD=2$\sqrt{34}$.
如图四边形ABCD中,AB=4$\sqrt{2}$,BC=12,∠ABC=45°,∠ADC=90°,AD=CD,则BD=2$\sqrt{34}$.
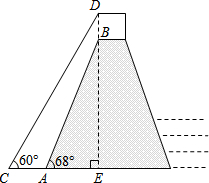 我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到173米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为B,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC.
我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到173米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为B,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC.