Question

6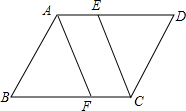．如图所示，平行四边形ABCD中，点E、F分别为边AD与CB的三等分点，试证明：
（1）四边形AFCE为平行四边形；
（2）△ABF≌△CDE．

Answer 1

分析 （1）直接利用平行四边形的对边平行且相等，进而得出AE$\stackrel{∥}{=}$FC，即可得出答案；
（2）利用平行四边形的性质得出AB=DC，AD=BC，∠B=∠D，进而结合全等三角形的判定方法得出答案．

解答 证明：（1）∵四边形ABCD是平行四边形，
∴AD$\stackrel{∥}{=}$BC，
∵点E、F分别为边AD与CB的三等分点，
∴AE=$\frac{1}{3}$AD，FC=$\frac{1}{3}$BC，
∴AE$\stackrel{∥}{=}$FC，
∴四边形AFCE为平行四边形；

（2）∵四边形ABCD是平行四边形，
∴AB=DC，AD=BC，∠B=∠D，
∵点E、F分别为边AD与CB的三等分点，
∴DE=$\frac{2}{3}$AD，FB=$\frac{2}{3}$BC，
∴BF=DE，
在△ABF和△CDE中
∵$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠D}\\{BF=DE}\end{array}\right.$，
∴△ABF≌△CDE．

点评 此题主要考查了平行四边形的判定与性质以及全等三角形的判定与性质，正确应用平行四边形的性质是解题关键．