题目内容
3.在△ABC中,∠C=90°,AC=3BC,则sinA=$\frac{\sqrt{10}}{10}$,cosA=$\frac{3\sqrt{10}}{10}$,tanA=$\frac{1}{3}$.分析 根据勾股定理,可得AB与BC的关系.根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
解答 解:由勾股定理,得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{10}$BC,
sinA=$\frac{BC}{AB}$=$\frac{\sqrt{10}}{10}$,cosA=$\frac{AC}{AB}$=$\frac{3\sqrt{10}}{10}$,tanA=$\frac{BC}{AC}$=$\frac{1}{3}$,
故答案为:$\frac{\sqrt{10}}{10}$,$\frac{3\sqrt{10}}{10}$,$\frac{1}{3}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
14.用计算器求sin28°,cos27°,tan26°的值,它们的大小关系是( )
| A. | tan26°<cos27°<sin28° | B. | tan26°<sin28°<cos27° | ||
| C. | sin28°<tan26°<cos27° | D. | cos27°<sin28°<tan26° |
 如图,测得某楼梯的长为5m,高为3m,宽为2m,计划在表面铺地毯,若每平方米地毯50元,你能帮助算出至少需要多少钱吗?
如图,测得某楼梯的长为5m,高为3m,宽为2m,计划在表面铺地毯,若每平方米地毯50元,你能帮助算出至少需要多少钱吗?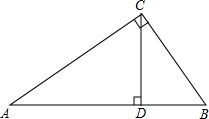 如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,则tanA=$\frac{BC}{AC}$=$\frac{CD}{AD}$,tanB=$\frac{AC}{BC}$=$\frac{CD}{BD}$,tan∠ACD=tanB,tan∠BCD=tanA.
如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,则tanA=$\frac{BC}{AC}$=$\frac{CD}{AD}$,tanB=$\frac{AC}{BC}$=$\frac{CD}{BD}$,tan∠ACD=tanB,tan∠BCD=tanA.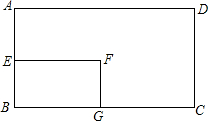 如图,矩形ABCD的面积是72,AE=$\frac{1}{2}$DC,EF=$\frac{1}{2}$AD,那么矩形EBGF的面积是( )
如图,矩形ABCD的面积是72,AE=$\frac{1}{2}$DC,EF=$\frac{1}{2}$AD,那么矩形EBGF的面积是( )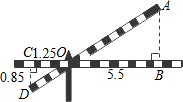 如图,铁道口的栏杆的短臂长1.25米,长臂长5.5米,当短臂端点下降0.85米时,长臂端点升高多少米?
如图,铁道口的栏杆的短臂长1.25米,长臂长5.5米,当短臂端点下降0.85米时,长臂端点升高多少米?