题目内容
18.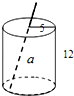 如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )| A. | 5≤a≤12 | B. | 5≤a≤13 | C. | 12≤a≤13 | D. | 12≤a≤15 |
分析 如图,当吸管底部在O点时吸管在罐内部分a最短,此时a就是圆柱形的高;当吸管底部在A点时吸管在罐内部分a最长,此时a可以利用勾股定理在Rt△ABO中即可求出.
解答  解:如图,
解:如图,
当吸管底部在O点时吸管在罐内部分a最短,
此时a就是圆柱形的高,
即a=12;
当吸管底部在A点时吸管在罐内部分a最长,
即线段AB的长,
在Rt△ABO中,AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴此时a=13,
所以12≤a≤13.
故选:C.
点评 本题考查正确运用勾股定理.善于观察题目的信息,正确理解题意是解题的关键.

练习册系列答案
相关题目
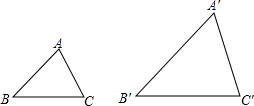 如图,已知△ABC∽△A′B′C′,且相似比为$\frac{AB}{A′B′}$=$\frac{3}{4}$,若AB=6,BC=5,AC=4,求△A′B′C′的周长.
如图,已知△ABC∽△A′B′C′,且相似比为$\frac{AB}{A′B′}$=$\frac{3}{4}$,若AB=6,BC=5,AC=4,求△A′B′C′的周长. 如图,已知A,B,C,D是⊙O上四点,若AC=BD,求证:AB=CD.
如图,已知A,B,C,D是⊙O上四点,若AC=BD,求证:AB=CD. 如图,测得某楼梯的长为5m,高为3m,宽为2m,计划在表面铺地毯,若每平方米地毯50元,你能帮助算出至少需要多少钱吗?
如图,测得某楼梯的长为5m,高为3m,宽为2m,计划在表面铺地毯,若每平方米地毯50元,你能帮助算出至少需要多少钱吗?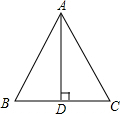 在△ABC中,AB=AC,AD是底边上的高,如图,若AC=6cm,AD=5cm,求BD的值.(精确到0.01cm)
在△ABC中,AB=AC,AD是底边上的高,如图,若AC=6cm,AD=5cm,求BD的值.(精确到0.01cm)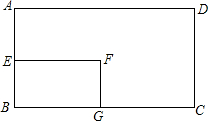 如图,矩形ABCD的面积是72,AE=$\frac{1}{2}$DC,EF=$\frac{1}{2}$AD,那么矩形EBGF的面积是( )
如图,矩形ABCD的面积是72,AE=$\frac{1}{2}$DC,EF=$\frac{1}{2}$AD,那么矩形EBGF的面积是( )