题目内容
4.在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的周长为( )| A. | 2$\sqrt{7}$ | B. | 4$\sqrt{7}$ | C. | 20 | D. | 40 |
分析 由菱形ABCD,根据菱形的对角线互相平分且垂直,可得AC⊥BD,OA=OC,OB=OD,易得AB=5;根据菱形的四条边都相等,即可得菱形的周长.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=3,OB=OD=$\frac{1}{2}$BD=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵AB=BC=CD=AD,
∴菱形的周长L=4AB=20.
故选C.
点评 此题考查了菱形的性质:菱形的对角线互相平分且垂直;菱形的四条边都相等.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
12.下列二次根式能与$\sqrt{6}$合并的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{8}$ | C. | $\sqrt{24}$ | D. | $\sqrt{30}$ |
16.下列图形既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.平行四边形ABCD中,∠A:∠B:∠C:∠D可能是( )
| A. | 2:1:2:1 | B. | 1:2:2:1 | C. | 2:1:1:2 | D. | 1:2:3:4 |
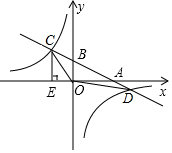 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E.
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的纵坐标为8.
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的纵坐标为8. 如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为24,则BC的长为( )
如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为24,则BC的长为( ) 如图,在平面直角坐标系xOy中,菱形ABCD的四个顶点都在格点上,且点A、B的坐标分别为(1,2)、(3,1)请解答下列问题:
如图,在平面直角坐标系xOy中,菱形ABCD的四个顶点都在格点上,且点A、B的坐标分别为(1,2)、(3,1)请解答下列问题: