题目内容
15.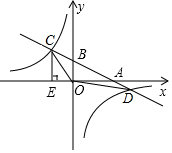 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E.
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E.(1)直接写出一次函数y=kx+b的表达式;
(2)根据图象,直接写出当自变量x取何值时,一次函数y=kx+b的值大于反比例函数y=-$\frac{24}{x}$的值;
(3)求△OCD的面积.
分析 (1)把(-4,m),代入y=-$\frac{24}{x}$得到C点坐标为(-4,6),然后解方程组即可得到结论;
(2)根据函数的图象即可得到结论;
(3)根据三角形的面积公式即可得到结论.
解答 解:(1)把(-4,m),代入y=-$\frac{24}{x}$得m=6,
∴C点坐标为(-4,6),
把C点坐标为(-4,6),D点坐标为(12,-2)代入y=kx+b得$\left\{\begin{array}{l}{6=-4k+b}\\{-2=12k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{1}{4}}\\{b=5}\end{array}\right.$,
∴一次函数y=kx+b的表达式为y=-$\frac{1}{4}$x+5;
(2)由图象知;当自变量x<-4或0<x<12时,一次函数y=kx+b的值大于反比例函数y=-$\frac{24}{x}$的值;
(3)∵B(0,5),
∴OB=5,
∴△OCD的面积=S△COB+S△DOB=$\frac{1}{2}$×5×4$+\frac{1}{2}$×5×12=40.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求一次函数的解析式,三角形的面积的计算,掌握的识别图象是解题的关键.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
10.下列计算中,正确的是( )
| A. | (x3)4=x7 | B. | x3+x4=x7 | C. | (-x)3(-x)4=x7 | D. | x5÷x3=x2 |
4.在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的周长为( )
| A. | 2$\sqrt{7}$ | B. | 4$\sqrt{7}$ | C. | 20 | D. | 40 |
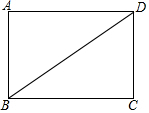 矩形ABCD的两边分别为AB=2$\sqrt{3}$厘米,BC=6厘米,求对角线BD的长和矩形ABCD的面积.
矩形ABCD的两边分别为AB=2$\sqrt{3}$厘米,BC=6厘米,求对角线BD的长和矩形ABCD的面积. 如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.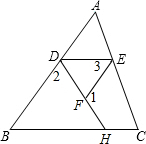 完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.