题目内容
12.下列二次根式能与$\sqrt{6}$合并的是( )| A. | $\sqrt{12}$ | B. | $\sqrt{8}$ | C. | $\sqrt{24}$ | D. | $\sqrt{30}$ |
分析 先化简各二次根式,然后找出被开方数为6的二次根式即可.
解答 解:A、$\sqrt{12}$=2$\sqrt{3}$,$\sqrt{12}$与$\sqrt{6}$不能合并;
B、$\sqrt{8}$=2$\sqrt{2}$,$\sqrt{8}$与$\sqrt{6}$不能合并;
C、$\sqrt{24}$=2$\sqrt{6}$,$\sqrt{24}$与$\sqrt{6}$能合并;
D、$\sqrt{30}$与$\sqrt{6}$不能合并.
故选:C.
点评 本题主要考查的是二次根式的化简、同类二次根式的定义,熟练掌握相关知识是解题的关键.

练习册系列答案
相关题目
17.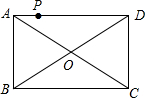 如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )
如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )
 如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )
如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )| A. | 4.8 | B. | 5 | C. | 6 | D. | 7.2 |
4.在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的周长为( )
| A. | 2$\sqrt{7}$ | B. | 4$\sqrt{7}$ | C. | 20 | D. | 40 |
2.父子二人并排竖直站立于游泳池中时,爸爸露出水面的高度是他自身身高的$\frac{1}{3}$,儿子露出水面的高度是他自身身高的$\frac{1}{4}$,父子二人的身高之和为3.4米.若设爸爸的身高为x米,儿子的身高为y米,则可列方程组( )
| A. | $\left\{\begin{array}{l}{x+y=3.4}\\{\frac{1}{3}x=\frac{1}{4}y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=3.4}\\{(1-\frac{1}{3})x=\frac{1}{4}y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=3.4}\\{\frac{1}{3}x=(1-\frac{1}{4})y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=3.4}\\{(1-\frac{1}{3})x=(1-\frac{1}{4})y}\end{array}\right.$ |
 如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.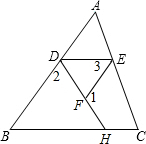 完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.