题目内容
14.关于x,y的方程组$\left\{\begin{array}{l}{2x+y=k}\\{x-y=1}\end{array}\right.$的解中,x>1,y≤1,求k的取值.分析 先解出方程组的解,然后利用条件列出不等式组即可求出k的范围.
解答 解:由方程组可知:$\left\{\begin{array}{l}{x=\frac{k+1}{3}}\\{y=\frac{k-2}{3}}\end{array}\right.$
∵x>1,y≤1,
∴$\left\{\begin{array}{l}{\frac{k+1}{3}>1}\\{\frac{k-2}{3}≤1}\end{array}\right.$
解得:2<k≤5
点评 本题考查学生的计算能力,解题的关键是熟练运用方程组与不等式组的解法,本题属于中等题型.

练习册系列答案
相关题目
4. 如图,直线l∥n,AB∥CD,∠1=30°,则∠2=( )
如图,直线l∥n,AB∥CD,∠1=30°,则∠2=( )
 如图,直线l∥n,AB∥CD,∠1=30°,则∠2=( )
如图,直线l∥n,AB∥CD,∠1=30°,则∠2=( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
19.下列各式的计算中,正确的是( )
| A. | $\sqrt{(-16)×(-25)}$=$\sqrt{(-16)}$×$\sqrt{(-25)}$=20 | B. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 | ||
| C. | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{81×1}$=9 | D. | 3$\sqrt{\frac{2}{3}}$=$\sqrt{2}$ |
4.在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的周长为( )
| A. | 2$\sqrt{7}$ | B. | 4$\sqrt{7}$ | C. | 20 | D. | 40 |
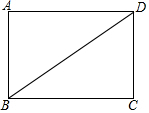 矩形ABCD的两边分别为AB=2$\sqrt{3}$厘米,BC=6厘米,求对角线BD的长和矩形ABCD的面积.
矩形ABCD的两边分别为AB=2$\sqrt{3}$厘米,BC=6厘米,求对角线BD的长和矩形ABCD的面积.