题目内容
13. 如图,在平面直角坐标系xOy中,菱形ABCD的四个顶点都在格点上,且点A、B的坐标分别为(1,2)、(3,1)请解答下列问题:
如图,在平面直角坐标系xOy中,菱形ABCD的四个顶点都在格点上,且点A、B的坐标分别为(1,2)、(3,1)请解答下列问题:(1)写出点C、D的坐标;
(2)画出菱形ABCD关于y轴对称的四边形A1B1C1D1,并写出点A1的坐标;
(3)画出菱形ABCD关于原点O对称的四边形A2B2C2D2,并写出点B2的坐标.
分析 (1)根据图象即可得到结论;
(2)根据关于y轴对称的点的坐标特点画出四边形A1B1C1D1即可;
(3)根据关于原点O对称的点的坐标特点即可得到四边形ABCD关于原点O对称的四边形A2B2C2D2.
解答 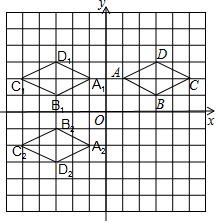 解:(1)C(5,2),D(3,3);
解:(1)C(5,2),D(3,3);
(2)如图所示,四边形A1B1C1D1即为所求;A1(-1,2);
(3)如图所示,四边形A2B2C2D2即为所求;B2(-3,-1).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了轴对称变换.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
4.在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的周长为( )
| A. | 2$\sqrt{7}$ | B. | 4$\sqrt{7}$ | C. | 20 | D. | 40 |
2.父子二人并排竖直站立于游泳池中时,爸爸露出水面的高度是他自身身高的$\frac{1}{3}$,儿子露出水面的高度是他自身身高的$\frac{1}{4}$,父子二人的身高之和为3.4米.若设爸爸的身高为x米,儿子的身高为y米,则可列方程组( )
| A. | $\left\{\begin{array}{l}{x+y=3.4}\\{\frac{1}{3}x=\frac{1}{4}y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=3.4}\\{(1-\frac{1}{3})x=\frac{1}{4}y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=3.4}\\{\frac{1}{3}x=(1-\frac{1}{4})y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=3.4}\\{(1-\frac{1}{3})x=(1-\frac{1}{4})y}\end{array}\right.$ |
3.每年四月北京很多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰.据测定,杨絮纤维的直径约为0.000 010 5米,将0.000 010 5用科学记数法可表示为( )
| A. | 1.05×105 | B. | 1.05×10-5 | C. | 0.105×10-4 | D. | 10.5×10-6 |
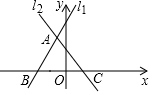 如图直线l1:y=2x+4与直线l2:y=-2x+2相交于点A,且直线l1,l2分别交x轴于点B和C.
如图直线l1:y=2x+4与直线l2:y=-2x+2相交于点A,且直线l1,l2分别交x轴于点B和C.