题目内容
19. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的纵坐标为8.
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的纵坐标为8.
分析 以正方形最外边上的点为准考虑,点的总个数等于最右边上的横坐标的平方,且横坐标为奇数时最后一个点在x轴上,为偶数时,从x轴上的点开始排列,求出与2017最接近的平方数为2025,然后得出第2017个点的坐标即可.
解答 解:根据图形可知:以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
右下角的点的横坐标为1,共有1个,即1=12,
右下角的点的横坐标为2时,共有4个,即4=22,
右下角的点的横坐标为3时,共有9个,即9=32,
…
右下角的点的横坐标为n时,共有n2个,
442=1936,452=2025,
根据规律可知:当n为奇数时,最后以点(n,0)结束;当n为偶数时,最后以点(1,n-1)结束;
∵n=45为奇数,
∴该正方形每一边上有45个点,且最后一个点的坐标为(45,0),是第2025个点,
∴第2017个点是从第2025个点向上数第8个点,
∴第2017个点的坐标为(45,8),
∴第2017个点的纵坐标为8,
故答案为:8.
点评 本题考查了点的坐标的规律变化,从正方形的观点考虑求解更简便,解决问题的关键是把握每一个正方形的最右边的点,要注意正方形的右边的点的横坐标是奇数还是偶数时,点的规律的不同.

练习册系列答案
相关题目
10.下列计算中,正确的是( )
| A. | (x3)4=x7 | B. | x3+x4=x7 | C. | (-x)3(-x)4=x7 | D. | x5÷x3=x2 |
14.放学以后,小明和小强从学校分手,分别沿东南方向和西南方向回家,若小明和小强行走的速度都是40米/分,小明用15分钟到家,小强用20分钟到家,小明家和小强家的距离为( )
| A. | 600米 | B. | 800米 | C. | 1000米 | D. | 不能确定 |
4.在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的周长为( )
| A. | 2$\sqrt{7}$ | B. | 4$\sqrt{7}$ | C. | 20 | D. | 40 |
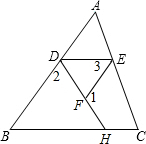 完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.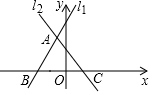 如图直线l1:y=2x+4与直线l2:y=-2x+2相交于点A,且直线l1,l2分别交x轴于点B和C.
如图直线l1:y=2x+4与直线l2:y=-2x+2相交于点A,且直线l1,l2分别交x轴于点B和C.