题目内容
16.在△ABC中,D、E分别是AB、AC的中点,F、G分别是DB、EC的中点,如果FG=3,那么BC=4.分析 设BC=2x,根据三角形的中位线平行于第三边并且等于第三边的一半表示出DE,再根据梯形的中位线平行于两底边并且等于两底和的一半列方程求解即可.
解答  解:设BC=2x,
解:设BC=2x,
∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC且DE=$\frac{1}{2}$BC=x,
∴四边形BCED是梯形,
∵F、G分别是DB、EC的中点,
∴FG是梯形BCED的中位线,
∴FG=$\frac{1}{2}$(DE+BC),
∵FG=3,
∴$\frac{1}{2}$(x+2x)=3,
解得x=2,
2x=2×2=4,
即BC=4.
故答案为:4.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,梯形的中位线平行于两底边并且等于两底和的一半,熟练掌握两个定理是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
11. 如图,?ABCD的周长为40,△BOC的周长比△AOB的周长多4,则AB的长为( )
如图,?ABCD的周长为40,△BOC的周长比△AOB的周长多4,则AB的长为( )
 如图,?ABCD的周长为40,△BOC的周长比△AOB的周长多4,则AB的长为( )
如图,?ABCD的周长为40,△BOC的周长比△AOB的周长多4,则AB的长为( )| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
1.某扇形的面积为3π,半径为6,此扇形的弧长为( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
8.某纪念品原价16元,连续两次降价a%后售价9元,下列所列方程正确的是( )
| A. | 16(1+a%)2=9 | B. | 16(1-a%)2=9 | C. | 16(1-2a%)=9 | D. | 16(1-a%)=9 |

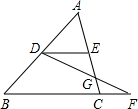 如图,在△ABC中,D、E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G,CF=2,则BC=4.
如图,在△ABC中,D、E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G,CF=2,则BC=4.