题目内容
19.有三个质地、大小都相同的小球分别标上数字2,-2,3后放入一个不透明的口袋搅匀,任意摸出一个小球,记下数字a后,放回口袋中搅匀,再任意摸出一个小球,又记下数字b.这样就得到一个点的坐标(a,b).(1)求这个点(a,b)恰好在函数y=-x的图象上的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)如果再往口袋中增加n(n≥1)个标上数字2的小球,按照同样的操作过程,所得到的点(a,b)恰好在函数y=-x的图象上的概率是$\frac{2(n+1)}{(n+3)^{2}}$(请用含n的代数式直接写出结果).
分析 (1)首先根据题意列出表格,然后由表格即可求得所有等可能的结果与这个点(a,b)恰好在函数y=-x的图象上的情况,再利用概率公式即可求得答案;
(2)由再往口袋中增加n(n≥1)个标上数字2的小球,共有(n+3)2种等可能的结果,其中符合要求的结果有2(n+1)种,直接利用概率公式求解即可求得答案.
解答 解:(1)列表得:
| a b | 2 | -2 | 3 |
| 2 | (2,2) | (2,-2) | (2,3) |
| -2 | (-2,2) | (-2,-2) | (-2,3) |
| 3 | (3,2) | (3,-2) | (3,3) |
∴P(点在函数图象上)=$\frac{2}{9}$;
(2)∵再往口袋中增加n(n≥1)个标上数字2的小球,共有(n+3)2种等可能的结果,其中符合要求的结果有2(n+1)种,
故答案为:$\frac{2(n+1)}{(n+3)2}$.
点评 此题考查了列表法或树状图法求概率.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
14.下列各图中,描述∠1与∠2互为余角关系最准确的是( )
| A. |  | B. |  | C. |  | D. |  |
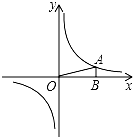 如图,在直角坐标系中,O为坐标原点.已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为$\frac{1}{2}$.
如图,在直角坐标系中,O为坐标原点.已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为$\frac{1}{2}$. 如图,如果曲线l1是反比例函数y=$\frac{k}{x}$在第一象限内的图象,且过点A(2,1),那么l1关于x轴对称的曲线l2的解析式为y=-$\frac{2}{x}$.
如图,如果曲线l1是反比例函数y=$\frac{k}{x}$在第一象限内的图象,且过点A(2,1),那么l1关于x轴对称的曲线l2的解析式为y=-$\frac{2}{x}$.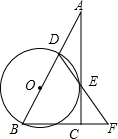 在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F,且BD=BF.
在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F,且BD=BF.