题目内容
18.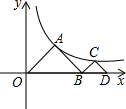 如图,△AOB,△CBD是等腰直角三角形,点A、C在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OB,BD都在x轴上,则点D的横坐标是4$\sqrt{2}$.
如图,△AOB,△CBD是等腰直角三角形,点A、C在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OB,BD都在x轴上,则点D的横坐标是4$\sqrt{2}$.
分析 过A作AE⊥x轴于E,过点C作CF⊥x轴于F,根据等腰直角三角形的性质得到OE=AE=BE,设OE=a,则A点坐标为(a,a),把它代入y=$\frac{4}{x}$(x>0)可求得a的值,而OB=2a,从而确定B点坐标;同理可设P2(4+b,b),求出b的值即可得出结论.
解答 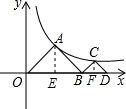 解:过A作AE⊥x轴于E,过点C作CF⊥x轴于F,如图
解:过A作AE⊥x轴于E,过点C作CF⊥x轴于F,如图
∵△AOB是等腰直角三角形,
∴OE=AE=BE,设OE=a,则A点坐标为(a,a),
∵点A在函数y=$\frac{4}{x}$(x>0)的图象上,
∴a2=4,
∴a=2,
∴OB=2a=4,
∴B点坐标为(4,0).
同理,设BF=b,则C(4+b,b),
∴b(4+b)=4,解得b1=-2+2$\sqrt{2}$,b2=-2-2$\sqrt{2}$(舍去),
∴BD=2(-2+2$\sqrt{2}$)=-4+2$\sqrt{2}$,
∴OD=4-4+4$\sqrt{2}$=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
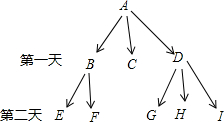 A同学心里有一个秘密,这个秘密按图中箭头指向在A,B,C,D,E,F,G,H,I这9个同学中传播,将这个秘密告诉过B的同学或者B将这个秘密告诉过的同学都不会再告诉B这个秘密.(注:不同的字母代表不同的同学)
A同学心里有一个秘密,这个秘密按图中箭头指向在A,B,C,D,E,F,G,H,I这9个同学中传播,将这个秘密告诉过B的同学或者B将这个秘密告诉过的同学都不会再告诉B这个秘密.(注:不同的字母代表不同的同学)