题目内容
11. 如图,平面直角坐标系中,A(4,2)、B(3,0),将△ABO绕OA中点C逆时针旋转90°得到△A′B′O′,连接OA′,则四边形OA′B′B的面积为6.5.
如图,平面直角坐标系中,A(4,2)、B(3,0),将△ABO绕OA中点C逆时针旋转90°得到△A′B′O′,连接OA′,则四边形OA′B′B的面积为6.5.
分析 过A'作O'B'的垂线交y轴于点N,由旋转性质得A'M=2,即可知A'N=MN-A'M=1、OA=2$\sqrt{5}$,根据C为OA中点得A'C=OC=$\sqrt{5}$,求得OA'=$\sqrt{10}$、ON=3,再求得B′M=$\sqrt{A′B{′}^{2}-A′{M}^{2}}$=1,根据S四边形OA′B′B=S矩形OBMN-S△A′NO-S△A′B′M即可求得答案.
解答 解:如图过A'作O'B'的垂线交y轴于点N,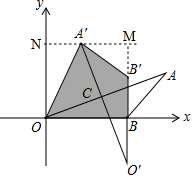
∵点A到OB的距离是2,
∴点A'到O'B'的距离A'M=2,
故A'N=MN-A'M=OB-A'M=3-2=1,
由勾股定理得OA=2$\sqrt{5}$,
∴A'C=OC=$\sqrt{5}$,
由勾股定理OA'=$\sqrt{10}$,
在Rt△OA'N中,用勾股定理得ON=3,
∵A′B′=AB=$\sqrt{(3-4)^{2}+(0-2)^{2}}$=$\sqrt{5}$,
∴B′M=$\sqrt{A′B{′}^{2}-A′{M}^{2}}$=$\sqrt{(\sqrt{5})^{2}-{2}^{2}}$=1,
则S四边形OA′B′B=S矩形OBMN-S△A′NO-S△A′B′M
=3×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2
=6.5,
故答案为:6.5.
点评 本题主要考查坐标与图形的变化-旋转,抓住旋转的三要素:旋转中心C,旋转方向逆时针,旋转角度90°,求得ON、A′M的长是解题的关键.

练习册系列答案
相关题目
3. 如图,在△ABC中,DE∥BC,AE=3,AC=9,AD=4,则AB的值为( )
如图,在△ABC中,DE∥BC,AE=3,AC=9,AD=4,则AB的值为( )
 如图,在△ABC中,DE∥BC,AE=3,AC=9,AD=4,则AB的值为( )
如图,在△ABC中,DE∥BC,AE=3,AC=9,AD=4,则AB的值为( )| A. | 6 | B. | 8 | C. | 9 | D. | 12 |

 将△ABC沿BC的方向平移得到△DEF.
将△ABC沿BC的方向平移得到△DEF.