题目内容
1.如果等腰三角形的周长是底边长的5倍,那么它的顶角的正弦值为$\frac{\sqrt{15}}{8}$.分析 设底边为a,由等腰三角形的周长是底边长的5倍,得出腰长为2a,再作出三角形的高AD和CE,根据三角形的面积公式得到CE=$\frac{BC•AD}{AB}$=$\frac{a•\frac{\sqrt{15}}{2}a}{2a}$=$\frac{\sqrt{15}}{4}$a,然后在直角△ACE中利用正弦函数的定义即可求出sin∠BAC的值.
解答 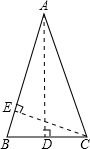 解:如图,等腰△ABC中,AB=AC,设底边BC为a.
解:如图,等腰△ABC中,AB=AC,设底边BC为a.
∵等腰三角形的周长是底边长的5倍,
∴腰长为2a,即AB=AC=2a.
作AD⊥BC于D点,CE⊥AB于E点,则BD=$\frac{1}{2}$a,
在Rt△ABD中,AD=$\sqrt{(2a)^{2}-(\frac{1}{2}a)^{2}}$=$\frac{\sqrt{15}}{2}$a,
∵S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$AB•CE,
∴CE=$\frac{BC•AD}{AB}$=$\frac{a•\frac{\sqrt{15}}{2}a}{2a}$=$\frac{\sqrt{15}}{4}$a,
∴sin∠BAC=$\frac{EC}{AC}$=$\frac{\frac{\sqrt{15}}{4}a}{2a}$=$\frac{\sqrt{15}}{8}$.
故答案为$\frac{\sqrt{15}}{8}$.
点评 本题考查了解直角三角形,等腰三角形的性质,三角形的面积,锐角三角函数定义,通过作辅助线构造直角三角形求出腰上的高CE是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
11.如图,是一个几何体的三视图(主视图中的弧线是半圆),则该几何体的体积是( )

| A. | π | B. | 2π | C. | 4π | D. | 8π |
9.某中学九年级(1)班体检结果出来后,一位同学对全班同学的身高(单位:厘米)统计如下表:
这组数据的众数为( )
| 身高(厘米) | 159 | 160 | 162 | 165 | 167 | 168 |
| 人数 | 3 | 5 | 8 | 18 | 10 | 8 |
| A. | 159 | B. | 162 | C. | 165 | D. | 167 |
13.有五条线段长度分别为1,3,5,7,9,从这5条线段中任取3条,则所取3条线段能构成一个三角形的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{10}$ |
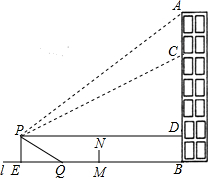 如图,重庆某广场新建与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直.在P处测得建筑物顶端A的仰角为37°,测得建筑物C处的仰角为26.6°(不计测量人员的身高),CD为25米.图中的点A、B、C、D、P及直线l均在同一平面内.
如图,重庆某广场新建与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直.在P处测得建筑物顶端A的仰角为37°,测得建筑物C处的仰角为26.6°(不计测量人员的身高),CD为25米.图中的点A、B、C、D、P及直线l均在同一平面内.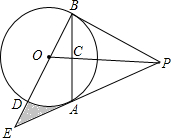 如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.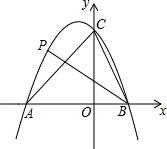 如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6).
如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6). 在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.
在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.