题目内容
8. 如图,点D是△ABC的外心,若∠DBC=40°,∠DBA=23°,则∠DCA的度数为27°.
如图,点D是△ABC的外心,若∠DBC=40°,∠DBA=23°,则∠DCA的度数为27°.
分析 根据外心的性质得到DB=DC,根据等腰三角形的性质得到∠DCB=∠DBC,求出∠BDC,根据圆周角定理求出∠A,根据三角形内角和定理计算即可.
解答 解:∵点D是△ABC的外心,
∴DB=DC,
∴∠DCB=∠DBC=40°,
∴∠BDC=100°,
∴∠A=$\frac{1}{2}$∠BDC=50°,
∴∠DCA=180°-40°-40°-50°-23°=27°,
故答案为:27°.
点评 本题考查的是三角形的外接圆与外心的概念和性质,掌握三角形外接圆的圆心是三角形三条边垂直平分线的交点是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
20.已知点(-2,y1),(-1,y2),(1,y3)都在反比例函数y=$\frac{k}{x}$(k<0)的图象上,那么y1,y2与y3的大小关系是( )
| A. | y3<y1<y2 | B. | y3<y2<y1 | C. | y1<y2<y3 | D. | y1<y3<y2 |
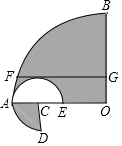 如图,扇形AOB与扇形DCE的圆心角分别为90°和270°,扇形DCE的弧过点A,FG∥AO,且与扇形DCE的弧相切,点F,G分别在弧AB,半径OB上,FG=2cm,则图中阴影部分的面积为πcm2.
如图,扇形AOB与扇形DCE的圆心角分别为90°和270°,扇形DCE的弧过点A,FG∥AO,且与扇形DCE的弧相切,点F,G分别在弧AB,半径OB上,FG=2cm,则图中阴影部分的面积为πcm2.